"Стоунхендж и пирамиды Египта" - читать интересную книгу автора (Фарлонг Девид)

Глава 4

Тайна углубляется

Возможно ли, что здесь, на земле Англии, оставлено геометрическое звено, связующее ее с самым знаменитым памятником античного мира?

Круг имеет точные геометрические пропорции. Зная длину радиуса или диаметра, можно вычислить его окружность и площадь. После установления этих величин для круга Марлборо-Даунс стало возможным сопоставить расстояния с известными древними единицами измерения вроде мегалитического ярда. В свое время это представлялось наиболее плодотворным путем исследования.

Профессор древней истории колледжа им. Уильяма Патерсона в Нью-Джерси Ливио Стеккини приводит — в Приложении к книге «Тайна Великой пирамиды» (Питера Томпкинса) — убедительные доказательства того, что древние народы имели представление о величине Земли и основывали на ней свои системы мер. В соответствии с его исследованием древние использовали главным образом пропорции, соотнесенные с длиной линии широты региона своего обитания. Эта поразительная, на первый взгляд, концепция в принципе не отличается от метрической системы. Изначально французы вычислили метр как одну десятимиллионную часть расстояния от полюса до экватора по меридиану, проходящему через Париж. Исследования Стеккини основывались главным образом на единицах измерения, использовавшихся в Древнем Египте, Вавилонии, Греции и Риме.

Меня заинтриговала идея профессора Стеккини о том, что народы древнего мира представляли себе размеры нашей планеты и соотносили с ними свои системы мер. Я рассуждал так: если мне удастся показать связь круга Марлборо с размерами Земли, тогда она увяжет его с другими древними единицами измерения и, следовательно, с другими культурами. Это существенным образом подтвердило бы, что круг является продуманным произведением, а не статистической случайностью. Это означало бы, что создатели круга обладали передовыми знаниями математики и, следовательно, могли быть профессиональными геодезистами, способными создать подобный рисунок на местности.

Исследование Стеккини подсказывало, что многие древние системы мер исходили из длины одного градуса широты. Она могла быть вычислена с помощью измерения длины тени и движения Солнца по сезонам. Поначалу я забыл или, скорее, упустил из виду тот факт, что Земля, круглая на экваторе, сплющена на полюсах. Это означает, что расстояния между линиями долготы всегда равны на каждой определенной широте, а расстояния между линиями широты меняются при передвижении от экватора к полюсу.

Упустив этот основной пункт, я решил для начала определить, существует ли какая-либо связь между длиной окружности экватора Земли и длиной окружности круга Марлборо. Из-за этой оплошности произошло нечто любопытное.

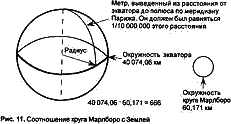
Известны несколько измерений окружности экватора, отличающиеся друг от друга на несколько сот метров. «Уорлд Альманак», например, указывает 40 074,06 километра (24 901,55 мили), что является приблизительно средней величиной по отношению к другим измерениям, и поэтому я выбрал ее. Рассчитанная окружность круга Марлборо равна 60,243 километра (37,433 мили). При делении на нее окружности экватора (40 074: 60,243 = 665,21) получаем число чуть больше 665.

Самая последняя спутниковая съемка, произведенная Международным союзом геодезии и геофизики, установила радиус Земли — 6378,136 километра +/— 1 метр. Разделив это число на радиус круга Марлборо (6 378 136: 9,558 = 665,22), я получил подтверждение первоначального расчета.

На первый взгляд, это не показалось мне существенным, пока я не подумал о загадочном числе 666 из Книги Откровения. Шанс на успех был невелик, но почему бы не предположить, что имелось в виду именно число 666? Как бы оно отразилось на величине круга?

Быстрый расчет показал: при уменьшении радиуса круга на 11 метров — с 9588 до 9576,78 метра получилось точное соответствие. Это было близко к предопределенной мной допустимой погрешности в десять метров и все еще соответствовало расположению объектов. Было ли это преднамеренно или еще одним простым совпадением? Как бы то ни было, что было такого особенного в числе 666?