"Элегантная вселенная (суперструны, скрытые размерности и поиски окончательной теории)" - читать интересную книгу автора (Грин Брайан)

Глава 12. За рамками струн: в поисках М-теории

В долгих поисках единой теории Эйнштейн размышлял о том, «мог ли Бог сотворить мир другим, оставляет ли какую-то свободу требование логической простоты»1). Это замечание Эйнштейна предвосхищает точку зрения, которой сегодня придерживаются многие физики: если у нас есть окончательная теория природы, то одним из самых убедительных аргументов в пользу ее конкретной структуры является то, что теория не могла бы быть другой. Окончательная теория должна иметь тот вид, который она имеет, потому что она дает уникальную формулировку, в рамках которой можно объяснить Вселенную, не натыкаясь на внутренние или логические противоречия. В подобной теории должно постулироваться, что все вокруг устроено именно так потому, что оно должно быть устроено именно так. Любое сколь угодно малое расхождение приводит к теории, которая, подобно фразе «это предложение является ложным», содержит в себе семена своей собственной несостоятельности.

Установление такой неизбежности в структуре Вселенной потребует долгого пути и вплотную приведет нас к разрешению глубочайших вопросов мироздания. Эти вопросы подчеркивают загадку: кто или что сделал выбор среди бессчетного числа вариантов? Неизбежность упраздняет эти вопросы путем отметания других возможностей. Неизбежность означает, что в действительности другого выбора нет. Неизбежность постулирует, что Вселенная не может быть иной. Как мы увидим в главе 14, нет причин, по которым Вселенная должна иметь такую жесткую конструкцию. Тем не менее, поиск этой жесткости законов природы лежит в основе программы объединения в современной физике.

К концу 1980-х гг. теория струн, по мнению физиков, хотя и приблизилась к построению единой картины Вселенной, но не выдержала экзамен на «отлично». На то были две причины. Во-первых, как вскользь отмечено в главе 7, физики обнаружили, что существует пять различных вариантов теории струн. Напомним, что их называют теориями типа I, типа IIА, типа IIВ, а также теориями гетеротических струн на основе групп О(32) (О-гетеротические струны) и Е8хЕ8 (Е-гетеротические струны). Многие основные свойства этих теорий совпадают: колебательные моды определяют возможные массы и заряды, общее число требуемых пространственных измерений равно 10, их свернутые измерения должны быть многообразиями Калаби-Яу и т.д. Мы не говорили об их различиях в предыдущих главах, однако, как выяснилось в конце 1980-х гг., эти теории действительно отличаются друг от друга. В примечаниях в конце книги можно прочесть о свойствах этих теорий, но здесь для нас важно то, что в них по-разному реализуется суперсимметрия и есть существенные различия между допустимыми колебательными модами2). (Например, в теории струн типа I кроме обсуждаемых нами замкнутых струн имеются открытые струны.) Теоретики, занимавшиеся струнами, чувствовали себя неуютно: хоть и впечатляет иметь на руках серьезную кандидатуру на окончательную единую теорию, но если таких кандидатур пять, непонятно, как распределить время на исследование каждой из них.

Вторая причина отклонения от неизбежности более тонкая. Чтобы понять ее в полной мере, нужно признать, что все физические теории состоят из двух частей. Первая часть — это набор основных идей теории, выраженных, как правило, в виде математических уравнений. Вторая часть состоит из решений этих уравнений. Вообще говоря, одни уравнения допускают только единственное решение, а другие — более одного решения (возможно, много более). (Например, уравнение «2 умножить на некоторое число равно 10» имеет одно решение: 5. Однако уравнение «0 умножить на некоторое число равно 0» имеет бесконечно много решений, так как любое умноженное на 0 число дает 0.) Тем самым, даже если получается строго определенная теория со строго определенными уравнениями, искомая неизбежность еще под вопросом, ибо уравнения могут иметь множество различных решений. В конце 1980-х гг. казалось, что ситуация в теории струн обстоит именно так. Когда физики начинали исследовать уравнения любой из пяти теорий, выяснялось, что у этих уравнений действительно много решений, например много возможных способов свертывания дополнительных измерений, и каждое решение соответствует вселенной со своими свойствами. И хотя все эти вселенные возникали в качестве полноправных решений уравнений теории струн, большинство из них, казалось, не имеет никакого отношения к наблюдаемому нами миру.

Эти отклонения от неизбежности могли бы считаться досадным фундаментальным недостатком теории струн. Но исследования, начавшиеся в середине 1990-х гг., дали надежду на то, что этот недостаток есть просто следствие того, как физики теоретики подходят к анализу теории струн. В двух словах, дело в том, что уравнения теории струн настолько сложны, что никто даже не знает их точного вида. Физикам удалось найти лишь приближенный вид этих уравнений. Именно эти приближенные уравнения сильно отличаются для разных теорий струн. И именно они в любом из пяти подходов приводят к избытку решений, рогу изобилия лишних вселенных.

С 1995 г. (начало второй революции в теории суперструн) растет число свидетельств в пользу того, что точные уравнения, вид которых до сих пор находится за пределами наших познаний, могут разрешить эти проблемы и, тем самым, придадут теории струн статус неизбежности. К удовлетворению большинства занимающихся теорией струн физиков уже доказано, что точные уравнения, когда их вид будет ясен, вскроют связь между всеми пятью теориями струн.

Как лучи морской звезды, все они являются частями одного организма, который в настоящее время пристально исследуется теоретиками. Физики уверены, что вместо пяти различных теорий должна существовать одна, объединяющая все пять в рамках общего теоретического формализма. Эта теория приведет к ясности, всегда возникающей при выявлении скрытых зависимостей между различными областями исследования, и даст новый мощный подход к пониманию структуры Вселенной в рамках теории струн.

Чтобы объяснить эти идеи, нам придется воспользоваться рядом самых сложных и самых современных результатов теории струн. Необходимо понять суть приближений, используемых в теории струн, а также присущие им ограничения. Нам нужно ближе познакомиться с искусными методами, известными под собирательным названием дуальностей, которые физики применяют для выхода за рамки некоторых приближений. Затем мы должны по шагам разобраться в каждом этапе аргументации, опирающейся на эти методы, и прийти к указанным выше замечательным выводам. Но не нужно пугаться: вся действительно сложная работа уже выполнена теоретиками, а нам остается лишь проиллюстрировать их результаты.

Тем не менее есть множество, казалось бы, не связанных элементов, которые нам придется исследовать и соединить воедино, поэтому в данной главе особенно просто не разглядеть за деревьями леса. Поэтому, если обсуждение в этой главе начнет казаться слишком запутанным и возникнет желание пропустить ее и перейти к черным дырам (главе 13) или космологии (главе 14), мы вам рекомендуем все-таки вернуться к следующему параграфу, где сведены вместе ключевые идеи второй революции в теории суперструн.

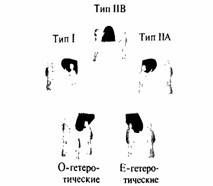
Важнейший результат, полученный в ходе второй революции в теории суперструн, показан на рис. 12.1 и 12.2. На рис. 12.1 изображена ситуация до того, как стало возможным (частично) выйти за рамки приближенных методов, традиционно используемых физиками для исследований в теории струн. Однако, как показано на рис. 12.2, в свете последних результатов видно, что подобно лучикам морской звезды все теории струн рассматриваются сейчас как части единого целого. (К концу этой главы, на самом деле, станет ясно, что даже и шестая теория — шестой лучик звезды — будет вписана в это объединение.)

Рис. 12.1. Многие годы физики, работавшие с пятью теориями струн, думали, что они исследукп совершенно различные теории.

Рис. 12.2. Результаты, полученные в ходе второй революции в теории суперструн, показали, что все пять теорий в действительности являются частью единого формализма, условно названного М-теорией.

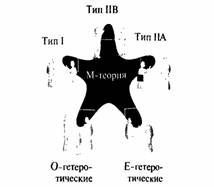Этот единый формализм по причинам, которые станут ясными в дальнейшем, условно назвали М-теорией. Рис. 12.2 иллюстрирует эпохальное достижение в поисках окончательной теории. Тропы исследований в теории струн, которые, казалось, ведут в разные стороны, слились в одну широкую дорогу — единую и всеохватывающую теорию, которая вполне может оказаться искомой «теорией всего».

Хотя предстоит проделать еще много работы, две основные характеристики М-теории уже установлены физиками. Во-первых, М-теория рассматривает одиннадцать измерений (десять пространственных и одно временное). Подобно тому, как Калуца внезапно обнаружил, что одно дополнительное пространственное измерение можно использовать для объединения гравитации с электромагнетизмом, теоретики осознали, что одно дополнительное пространственное измерение в теории струн (помимо оставшихся девяти пространственных и одного временного, обсуждавшихся в предыдущих главах) позволяет осуществить более чем удовлетворительный синтез всех пяти вариантов теории струн. Кроме того, это дополнительное измерение возникает не из воздуха: теоретики обнаружили, что выводы о существовании одного временного и девяти пространственных измерений, сделанные в 1970-х и 1980-х гг., являются приближенными, а точные вычисления показывают, что одно пространственное измерение в те годы осталось незамеченным.

Второе установленное свойство М-теории состоит в том, что она, кроме колеблющихся струн, включает и другие объекты: колеблющиеся двумерные мембраны и трехмерные капли (последние называют 3-бранами), а также и многие другие составляющие. Это свойство, как и одиннадцатое измерение, возникает вследствие отказа от приближений, использовавшихся до середины 1990-х гг. Если не считать этих и ряда других результатов, полученных в последние годы, М-теория остается мистической (этим объясняется одно из предложенных толкований буквы «М» в ее названии). Физики всего мира с большим энтузиазмом работают над тем, чтобы добиться полного понимания М-теории, и эта задача вполне может стать центральной проблемой физики XXI в.

Ограничения методов, с помощью которых физики пытались анализировать теорию струн, связаны с использованием теории возмущений. Теория возмущений — меткое название приближенной процедуры, в которой сначала пытаются найти грубый ответ, а затем поэтапно уточняют его с учетом все большего числа подробностей, опущенных на предыдущих этапах. Теория возмущений играет важную роль во многих областях науки; она являлась существенным элементом в понимания теории струн, и, как мы сейчас покажем, прочно входит в круг житейских явлений.

Предположим, что в один прекрасный день машина вашего знакомого начинает барахлить, и он обращается в мастерскую, чтобы ее проверить. Осмотрев машину, механик говорит, что дело плохо. Нужен новый блок двигателя, и обычно ремонт в таких случаях обходится примерно в $900 (включая стоимость деталей). Это примерная оценка, а более точная стоимость выяснится в ходе ремонта. Проходит несколько дней, и, проведя дополнительные проверки, механик сообщает более точную стоимость $950. Он объясняет, что необходим еще и новый регулятор: это увеличит общую стоимость ремонта примерно на $50. Наконец, когда машина отремонтирована, вашему знакомому выставляется счет на $987,93. В мастерской объясняют, что в него входят $950 за блок двигателя и регулятор, $27 за ремень вентилятора, $10 за кабель аккумулятора и $0,93 за изолированный болт. Примерная первоначальная стоимость $900 уточнялась с учетом все более мелких деталей. На языке физики эти детали рассматриваются как возмущения исходной оценки.

При правильном использовании теории возмущений первоначальная оценка будет достаточно близка к окончательному ответу, и после учета мелких подробностей, опущенных в исходной оценке, поправка будет невелика. Но иногда при оплате счета выясняется, что конечная сумма ужасающе расходится с начальной оценкой. И хотя в этот момент в голову, возможно, приходят совсем другие слова, в математике это называется неприменимостью теории возмущений. Это означает, что исходное приближение было плохим прогнозом окончательного ответа, потому что поправки привели не к относительно малым отклонениям, а к сильным изменениям приближенной оценки. Как указывалось в предыдущих главах, наше обсуждение теории струн до этого места опиралось на теорию возмущений, в определенном смысле аналогичную той, которую использовал механик. Упоминавшееся время от времени «недостаточное понимание» теории струн так или иначе связано с применением этого приближенного метода. Чтобы лучше понять смысл последнего утверждения, рассмотрим теорию возмущений в контексте, менее абстрактном, чем в теории струн, но все же более близком к этой теории, чем пример с механиком.

Классический пример использования теории возмущений дает изучение движения Земли в Солнечной системе. На таких больших пространственных масштабах можно учитывать только гравитационное взаимодействие, однако, если не делать дополнительных приближений, возникающие уравнения будут крайне сложны. Вспомним, что и по Ньютону, и по Эйнштейну все тела оказывают гравитационное воздействие на все другие тела, так что попытка точной формулировки сразу приводит к математически неразрешимой задаче о «гравитационном перетягивании каната» Землей, Солнцем, другими планетами и, если по-честному, всеми другими небесными телами. Как нетрудно сообразить, определить точное движение Земли с учетом всех влияний невозможно. На самом деле, уже в случае трех небесных тел уравнения становятся настолько сложными, что никто не сумел полностью решить их3'.

Тем не менее в рамках теории возмущений можно предсказать движение Земли в Солнечной системе с высочайшей точностью. Огромная масса Солнца по сравнению с массами всех других тел Солнечной системы, как и близость Солнца к Земле по сравнению с расстояниями от Земли до других звезд, свидетельствуют о том, что Солнце оказывает доминирующее воздействие на движение Земли. Таким образом, в первом приближении можно учитывать только гравитационное воздействие Солнца. Для многих приложений этого вполне достаточно. Если окажется необходимым, можно уточнить это приближение, последовательно учитывая гравитационное воздействие следующих по степени влияния тел, например, Луны или тех планет, которые в данный момент проходят ближе всего к Земле. По мере того как паутина гравитационных взаимодействий будет становиться более запутанной, вычисления могут стать сложными, но это не должно затемнять смысл философии теории возмущений: гравитационное взаимодействие между Землей и Солнцем дает нам приближенное понимание движения Земли, а совокупность остальных гравитационных взаимодействий последовательно учитывается все уменьшающимися поправками. В этом примере подход в рамках теории возмущений применим, так как существует доминирующее физическое воздействие, допускающее сравнительно простое теоретическое описание. Это не всегда так. Например, если нужно рассчитать движение трех сравнимых по массе звезд, вращающихся в тройной системе одна вокруг другой, нельзя указать, взаимодействие каких звезд будет доминирующим. Поэтому нельзя дать грубую оценку, к которой затем можно было бы делать малые поправки, обусловленные другими эффектами. Если попытаться использовать теорию возмущений и выбрать для грубой оценки, например, взаимодействие между двумя звездами, быстро выяснится, что подход неприменим. Вычисленные «поправки» за счет влияния третьей звезды будут не малыми, а столь же существенными, что и первое грубое приближение. Ситуация знакомая: движения трех человек, танцующих танец «хора» мало напоминают движения пары, танцующей танго. Большие поправки означают, что исходное приближение было выстрелом мимо цели, а вся схема была карточным домиком. Важно понимать, что дело не просто в учете большой поправки третьей звезды. Здесь действует эффект домино: большая поправка сильно влияет на движение двух звезд, что, в свою очередь, сильно влияет на движение третьей звезды, которое опять-таки влияет на движение двух звезд, и т. д. Все нити гравитационной паутины одинаково важны, и должны рассматриваться одновременно. Единственным спасением в таких случаях часто бывает метод грубой силы — компьютерное моделирование совместного движения.

Этот пример демонстрирует, насколько при использовании теории возмущений важно определить, является ли предполагаемое первое приближение действительно приближением, и, если оно им является, сколько и каких более точных деталей следует учитывать, для достижения требуемой точности. Как мы сейчас обсудим, эти вопросы особенно важны при применении теории возмущений к изучению физических процессов в микромире.

Физические процессы в теории струн порождаются фундаментальными взаимодействиями между колеблющимися струнами. Как обсуждалось в главе 6 (читателям, пропустившим раздел «Более точный ответ» в главе 6, рекомендуется пролистать его начало.), в эти взаимодействия входят распады и слияния струнных петель, подобные тем, которые изображены на рис. 6.7 и продублированы для удобства читателя на рис. 12.3. Занимающиеся струнами теоретики показали, как схематическому изображению на рис. 12.3 поставить в соответствие точную математическую формулу, описывающую влияние каждой из сталкивающихся струн на движение другой. (Эта формула имеет разный вид в пяти теориях струн, но мы на время будем пренебрегать такими тонкостями.)

Рис. 12.3. Струны взаимодействуют, соединяясь и разделяясь.

Если бы не было квантовой теории, на этой формуле и заканчивалось бы изучение взаимодействия струн. Но в силу соотношения неопределенностей возникает микроскопический хаос, в котором происходит непрерывное рождение пар струна/антиструна (двух струн с противоположными колебательными модами) за счет одолженной у Вселенной энергии, и быстрая аннигиляция этих пар, в результате которой одолженная энергия возвращается Вселенной. Такие пары струн, рожденные из квантового хаоса, живущие за счет одолженной энергии и, следовательно, обязанные быстро слиться в одну петлю, называют парами виртуальных струн. И хотя их жизнь скоротечна, присутствие этих дополнительных пар виртуальных струн влияет на детальную структуру взаимодействия.

Схематически этот процесс изображен на рис. 12.4. Две исходные струны сливаются вместе в точке а, образуя единую петлю. Некоторое время эта петля движется, но в точке б квантовые флуктуации приводят к рождению виртуальной пары струн, которая далее аннигилирует в точке в, и в результате снова получается одна петля.

Рис. 12.4. Квантовый хаос приводит к рождению пары струна/антиструна (6) и ее уничтожению (в), что усложняет взаимодействие.

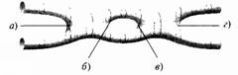Наконец, в точке г эта струна отдает энергию, распадаясь на пару струн, которые разлетаются в разных направлениях. Из-за наличия одной петли в центре рис. 12.4 физики называют это «однопетлевым» процессом. Как и для взаимодействия, изображенного на рис. 12.3, для этой диаграммы можно выписать точную математическую формулу, в которой учитывается влияние рождения пары виртуальных струн на движение двух исходных.

Однако это еще не все: краткосрочные извержения виртуальных струн вследствие квантовых флуктуации могут произойти любое число раз, что приведет к рождению последовательных виртуальных пар. При этом получатся диаграммы с большим количеством петель, как показано на рис. 12.5.

Рис. 12.5. Квантовый хаос может привести к рождению и уничтожению длинных последовательностей пар струна/антиструна.

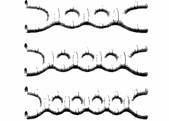Каждая диаграмма дает простой и удобный способ описания соответствующего физического процесса. Налетающие струны сливаются, квантовый хаос вызывает раздвоение получившейся петли на виртуальную пару, струны этой пары движутся, затем аннигилируют с образованием одной петли, которая далее снова распадается на виртуальную пару и т. д. Как и для других диаграмм, для каждого из этих процессов есть математические формулы, в которых учитывается влияние на движение исходной пары струн4).

Более того, аналогично примеру с механиком, определившим конечную стоимость ремонта сложением его исходной оценки $900 с последующими поправками $50, $27, $10 и $0,93, и аналогично уточнению описания движения Земли при добавлении к влиянию Солнца меньшего влияния Луны и других планет, теоретики показали, что взаимодействие двух струн можно вычислить путем сложения математических выражений для диаграмм без петель (без пар виртуальных струн), с одной петлей (одной парой виртуальный струн), с двумя петлями (двумя парами виртуальных струн) и т.д., как показано на рис. 12.6.

Рис. 12.6. Суммарное воздействие одной струны, налетающей на другую, есть результат сложения воздействий, включающих диаграммы с увеличивающимся числом петель.

В точном расчете требуется сложить математические выражения для всех этих диаграмм с растущим числом петель. Но так как диаграмм бесконечно много, а соответствующие математические вычисления с ростом числа петель усложняются, эта задача неразрешима. И здесь занимающиеся струнами теоретики берут на вооружение теорию возмущений, предполагая, что разумная грубая оценка дается процессом без петель, а диаграммы с петлями дают поправки, значения которых уменьшаются по мере увеличения числа петель.

В действительности, почти все, что мы знаем о теории струн, включая большую часть сведений из предыдущих глав, было открыто физиками при проведении подробных и тщательных вычислений по теории возмущений. Но чтобы удостовериться в точности полученных результатов, необходимо выяснить, являются ли грубые приближения, в которых учитывается только несколько первых диаграмм рис. 12.6, а все остальные диаграммы опущены, действительно хорошим приближением.

Нельзя сказать заранее. Хотя математические формулы, соответствующие диаграммам, значительно усложняются при увеличении числа петель, теоретикам удалось установить одно очень важное свойство. Подобно тому, как вероятность разрыва каната на две части при сильном растяжении и раскачивании определяется его прочностью, вероятность распада струны с образованием виртуальной пары при квантовых флуктуациях также определяется некоторым параметром. Этот параметр называют константой связи

струны (как мы вскоре увидим, в каждой из пяти теорий струн своя константа связи). Это название довольно наглядно: значение константы cвязи струны определяет, насколько сильно квантовые колебания трех струн (исходной струны и двух виртуальных струн, на которые она распадается) зависят друг от друга, т. е. насколько сильно три струны связаны между собой. Вычисления показывают, что при больших значениях константы связи струны вероятность того, что квантовые флуктуации приведут к распаду струны (и ее последующему воссоединению), становится больше, а при малых значениях константы связи вероятность такого краткосрочного образования виртуальных струн мала.

Немного ниже мы обсудим вопрос об определении константы связи струны в каждой из пяти теорий, однако сначала необходимо уточнить, что означают слова «большая» и «малая» применительно к константе связи. Оказывается, что с точки зрения математического формализма теории струн границей между областями «больших» и «малых» констант связи является число 1. Это означает, что при константах связи, меньших 1, молниеносное вырывание большого числа пар виртуальных струн становится крайне маловероятным. Однако если константа связи больше или равна 1, то краткосрочное появление на сцене таких виртуальных пар становится весьма вероятным и увеличивается с увеличением константы связи струны5). В итоге, при константах связи струны, меньших 1, вклады диаграмм с петлями при увеличении числа петель уменьшаются. Это как раз то, что нужно для подхода с использованием теории возмущений: уменьшение вкладов говорит о том, что мы получим достаточно точные результаты, если будем пренебрегать всеми вкладами, кроме вкладов диаграмм, содержащих лишь несколько петель. Но если константа связи струны больше 1, то по мере увеличения числа петель старшие петлевые вклады становятся все более важными. Как и в случае тройной системы звезд, теория возмущений здесь неприменима. И первое приближение, которое дают диаграммы без петель, приближением не является. (Все это в равной мере относится к каждой из пяти теорий струн, так как применимость приближенного подхода с использованием теории возмущений к любой заданной теории определяется значением константы связи.)

Поэтому возникает еще один важнейший вопрос: чему же равно значение константы связи (точнее, чему равны значения констант связи струны в каждой из пяти теорий струн)? Найти ответ до сих пор никому не удалось. Этот вопрос является одним из главных нерешенных вопросов в теории струн. Можно с уверенностью утверждать, что выводы, полученные в рамках теории возмущений, справедливы лишь в случае, если константа связи струны меньше единицы. Кроме того, точное значение константы связи струны непосредственно влияет на массы и заряды частиц, соответствующих ее различным колебательным модам. Таким образом, значение константы связи струны определяет большинство физических свойств теории. Сейчас мы подробнее обсудим причины того, почему на вопрос о значении константы связи во всех пяти теориях струн до сих пор нет ответа.

Как и для определения взаимодействия между струнами, для поиска фундаментальных уравнений теории струн может использоваться теория возмущений. На самом деле, эти уравнения определяют то, как струны взаимодействуют между собой, и, наоборот, способ взаимодействия струн определяет уравнения теории.

В каждой из пяти теорий струн существует уравнение, с помощью которого можно вычислить значение константы связи в этой теории. Однако к настоящему времени для всех пяти теорий физикам удалось найти лишь приближенный вид этого уравнения, полученный в рамках теории возмущений путем вычисления небольшого числа определенных диаграмм. И во всех пяти теориях приближенный вид уравнения говорит лишь о том, что если умножить значение константы связи на нуль, должен получиться нуль. Результат крайне удручающий, так как любое число при умножении на нуль дает нуль, и уравнению удовлетворяет любое значение константы связи струны. Поэтому во всех пяти теориях приближенные уравнения для определения константы связи не дают никакой информации о ее значении.

Кроме того, в каждой из пяти теорий струн должно существовать уравнение, с помощью которого в принципе можно определить точный вид как протяженных, так и свернутых пространственно-временных измерений. Известный на данный момент приближенный вид этого уравнения приводит к гораздо более жестким ограничениям, чем вид уравнения для константы связи, но допустимых решений все равно оказывается очень много. Например, допустимы решения с четырьмя протяженными и шестью свернутыми измерениями Калаби-Яу, но даже этим широким классом решений все они не исчерпываются: возможны и другие разбиения числа измерений на протяженные и свернутые6).

Что означают эти результаты? Возможны три ситуации. В первом, наихудшем случае даже при наличии уравнений для определения константы связи струны, а также уравнений для определения размерностей и точного вида пространства-времени (этим не может похвастаться ни одна теория), до сих пор не найденные точные уравнения могут допускать широкий спектр решений, что значительно ослабляет их предсказательную силу. Если это так, это будет крахом гипотезы о том, что теория струн способна объяснить свойства природы без необходимости экспериментального определения этих свойств и более или менее произвольной подгонки теории под эти свойства. Мы вернемся к анализу этого случая в главе 15. Во втором случае избыточная свобода выбора при решении приближенных уравнений теории струн может говорить об изъянах в нашей аргументации. Мы пытаемся использовать методы теории возмущений для определения значения самой константы связи струны. Но, как обсуждалось выше, методы теории возмущений имеют смысл лишь в случае, если константа связи меньше 1, и поэтому возможно, что при таких расчетах делается неоправданное предположение о самом результате, а именно, что этот результат будет меньше 1. Наша неудача вполне может объясняться неправильностью исходной предпосылки: в любой из пяти теорий струн константа связи может быть больше 1. Наконец, в третьем случае нежелательный произвол в решениях может быть просто следствием того, что мы используем приближенные, а не точные уравнения. Например, даже если константа связи в данной теории струн меньше 1, уравнения теории могут быть чувствительны к вкладам всех диаграмм. То есть учет небольших поправок, соответствующих всем многопетлевым диаграммам, может быть важным для сведения приближенного уравнения, допускающего множество решений, к точному уравнению с ограниченным числом решений.

К началу 1990-х гг. анализ двух последних возможностей убедил большинство теоретиков в том, что повсеместное использование теории возмущений является помехой на пути прогресса. По мнению подавляющего большинства ученых, следующее серьезное продвижение возможно лишь при использовании подхода, не скованного приближенными методами и, следовательно, далеко выходящего за рамки теории возмущений. Еще в 1994 г. разработка такого подхода казалась несбыточной мечтой. Однако иногда и такие мечты сбываются.

Сотни занимающихся теорией струн теоретиков из многих стран мира ежегодно съезжаются на конференцию, посвященную обсуждению полученных за «отчетный» год результатов и оценке перспектив возможных направлений исследования. В зависимости от достигнутого в данном году прогресса обычно легко предугадать степень интереса и энтузиазм его участников. В середине 1980-х гг., в апогее первой революции в теории суперструн, на семинарах царила безграничная эйфория. Физиков окрыляла надежда на то, что скоро у них появится полное понимание теории струн, и она предстанет пред ними в качестве окончательной теории Вселенной. Сегодня это кажется наивным. Как выяснилось в следующие годы, для понимания многих глубоких и нетривиальных аспектов теории струн требуются длительные и напряженные исследования. После того как далеко не все сразу становилось на свои места, необоснованная первоначальная эйфория сменилась мертвым сезоном, а многие исследователи впали в уныние. Конференции по струнам, проводившиеся в конце 1980-х гг., отражали скрытое разочарование: физики представляли интересные результаты, но в атмосфере конференции не чувствовалось вдохновения. Некоторые даже предлагали отменить ежегодную конференцию. Однако в начале 1990-х годов ситуация стала исправляться. После ряда значительных прорывов (некоторые из них обсуждались в предыдущих главах) теория струн вновь стала набирать свою силу, и у многих исследователей опять появился энтузиазм и оптимизм. Тем не менее, трудно было предположить то, что произойдет на конференции по струнам, состоявшейся в марте 1995 г. в университете Южной Калифорнии.

Когда подошло время заявленного выступления Эдварда Виттена, он поднялся на кафедру и сделал доклад, который вызвал вторую революцию в теории суперструн. Вдохновленный результатами более ранних работ Даффа, Халла и Таунсенда, а также замечательными идеями Шварца, Ашока Сена и других теоретиков, Виттен объявил о новой стратегии выхода за рамки теории возмущений в теории струн. Главным элементом этой стратегии было понятие дуальности.

Физики используют это понятие для описания теоретических моделей, которые кажутся различными, но приводят к идентичным физическим следствиям. Есть «тривиальные» примеры дуальности, в которых совершенно одинаковые теории могут казаться различными лишь вследствие того, как эти теории представлены. Человек, понимающий только английский язык, не поймет, что речь идет о теории относительности, если объяснять ему эту теорию на китайском языке. Однако физик, свободно владеющий обоими языками, легко переведет ее на свой язык и установит эквивалентность двух теорий. Мы называем этот пример «тривиальным», поскольку с точки зрения физики при переводе не обнаруживается ничего нового. Для владеющих разными языками теоретиков получить новый результат в теории относительности одинаково сложно вне зависимости от того, на каком языке эта теория сформулирована. Переход от английского к китайскому и обратно не приводит к появлению новых физических результатов.

Нетривиальными являются те примеры дуальности, в которых различные описания одной и той же ситуации приводят к различным взаимодополняющим физическим выводам и математическим методам исследования. На самом деле, выше мы уже дважды сталкивались с такими примерами. В главе 10 обсуждалось, что теория струн во вселенной с циклическим измерением радиусом R может быть с тем же успехом описана в рамках теории во вселенной с циклическим измерением радиусом 1/R. Геометрически два варианта различны, но физические явления оказываются совершенно идентичными. Второй пример — зеркальная симметрия. Имеются два различных многообразия Калаби-Яу в дополнительных шести пространственных измерениях, но две вселенные, кажущиеся на первый взгляд совершенно разными, имеют одни и те же физические свойства. Существенным отличием от перевода с одного языка на другой является то, что эти дуальные описания могут привести к новым физическим результатам, например, к предсказаниям минимального размера циклического измерения или переходов с изменением топологии в теории струн.

В своей лекции на конференции «Струны-95» Виттен привел пример нового и фундаментального типа дуальности. Как кратко отмечено в начале этой главы, он предположил, что пять теорий струн, имеющих совершенно разную структуру, на самом деле являются лишь разными способами описания одного и того же физического мира. Работая с пятью теориями струн, мы просто смотрели в пять разных окон, обращенных в сторону одного теоретического фундамента.

До событий середины 1990-х гг. возможность существования дуальности такого масштаба была одной из лелеемых физиками идей, о которой можно было упоминать лишь шепотом — настолько она представлялась фантастической. Если две теории существенно расходятся в деталях формулировки, трудно вообразить, что эти теории могут быть просто двумя разными описаниями одной и той же физической реальности, лежащей в основе. Тем не менее, с развитием теории струн появляются все более убедительные свидетельства в пользу того, что все пять теорий струн являются дуальными. Кроме того, как будет пояснено ниже, из доводов Виттена следует, что в физике есть место и для шестой теории.

Эти результаты тесно переплетены с вопросами о применимости методов теории возмущений, обсуждавшихся в конце предыдущего пункта. Причина в том, что пять теорий струн сильно отличаются друг от друга, если в каждой из них предполагается наличие слабой связи, т. е. если константа связи меньше 1. Долгое время физики опирались на теорию возмущений, в рамках которой невозможна постановка вопроса о том, какими будут свойства любой из теорий, если окажется, что константа связи в этой теории больше 1, т. е. связь будет сильной. По утверждениям Виттена и других исследователей, сейчас можно ответить на этот важнейший вопрос. Их результаты убедительно свидетельствуют о том, что для сильной связи в каждой из теорий (включая шестую теорию, которую мы опишем ниже) есть дуальное описание в терминах слабой связи в другой теории, и наоборот.

Чтобы яснее понять смысл последнего утверждения, можно взять на вооружение следующую аналогию. Представим себе двух, мягко говоря, слегка чудаковатых индивидуумов. Один из них обожает лед, но, как ни странно, никогда не видел воды. Второй обожает воду, но, что не менее странно, никогда не видел льда. Однажды они встречаются и решают отправиться в поход по пустыне. В начале похода каждый из них изумлен снаряжением другого. Любитель льда пленен гладкой поверхностью прозрачной жидкости, которую принес с собой любитель воды, а любителя воды странным образом притягивают твердые кубики, принесенные любителем льда. Ни один из них и не подозревает о близком родстве между льдом и водой; для них эти субстанции совершенно различны. Но, продвигаясь по палящей жаре пустыни, они поражены тем, что лед начинает медленно превращаться в воду. А позже, дрожа от дикого холода пустынной ночи, они столь же сильно поражены тем, что жидкая вода начинает медленно превращаться в твердый лед. И тут до них доходит, что вода и лед, которые они считали совершенно разными веществами, тесно связаны между собой.

Дуальность в пяти теориях струн в чем-то похожа на этот пример: грубо говоря, константы связи струны играют роль, аналогичную температуре в пустыне. Подобно воде и льду, любые две из пяти теорий с первого взгляда кажутся совершенно различными. Но при изменении соответствующих констант связи эти теории превращаются одна в другую. Так же, как лед превращается в воду при увеличении температуры, одна из теорий переходит в другую при увеличении константы связи. Эта аналогия, в конце концов, может привести нас к выводу о том, что все теории струн являются дуальными описаниями единой структуры — аналога Н2О для воды и льда.

Аргументация в пользу такого вывода почти целиком основана на принципах симметрии. Обсудим эти принципы.

Никто и никогда даже не пытался изучить свойства любой из пяти теорий струн при больших значениях констант связи, потому что не было и намека на то, как поступать вне рамок теории возмущений. Однако в конце 1980-х — начале 1990-х гг. физики начали делать первые, но твердые шаги к описанию конкретных свойств теорий (в частности, к вычислению отдельных масс и зарядов), проявляющихся в области физики сильной связи для данной теории, но все же находящихся в пределах наших вычислительных возможностей. Такие вычисления, с необходимостью выходившие за рамки теории возмущений, сыграли главную роль во второй революции суперструн и стали возможными во многом благодаря соображениям симметрии.

Принципы симметрии дают мощные средства для изучения многих свойств реального мира. Мы уже упоминали о том, что хорошо подтверждающаяся уверенность в том, что законы физики не выделяют никакое конкретное место во Вселенной и никакой конкретный момент времени, позволяет нам предположить, что законы «здесь и сейчас» будут теми же самыми, что и «там и тогда». Это всеобъемлющий пример; но принципы симметрии могут с тем же успехом применяться в более скромных случаях. Например, если свидетель ограбления разглядел лишь правую половину лица преступника, в полиции его информация все равно окажется ценной для составления фоторобота. Симметрия тому причиной. Хотя правая и левая половина лица отличаются, большинство лиц достаточно симметричны для того, чтобы отраженный образ одной половины лица можно было бы с успехом использовать в качестве приближения для другой половины.

В каждом из разнообразных применений роль симметрии состоит в возможности восстановления свойств по косвенным признакам, что часто гораздо проще прямого подхода. Для изучения законов физики в созвездии Андромеды можно было бы направить туда экспедицию, найти подходящую планету у одной из звезд, построить там ускорители и проводить эксперименты, аналогичные экспериментам на Земле. Но косвенный подход с использованием симметрии при сдвиге места действия куда проще. Можно было бы в деталях ознакомиться с чертами левой половины лица грабителя, изловив преступника и отправив его в участок. Но часто гораздо проще сначала воспользоваться лево-правой симметрией человеческих лиц7).

Суперсимметрия принадлежит к более абстрактным типам симметрии, который связывает физические свойства элементарных объектов с различными спинами. Эксперимент дает лишь косвенные намеки на то, что в микромире реализуется такой механизм симметрии, но по описанным выше причинам физики твердо убеждены, что он действительно реализуется. Естественно, этот механизм является неотъемлемой частью теории струн. В 1990-е гг. после пионерской работы Натана Зайберга из Института перспективных исследований физики осознали, что суперсимметрия дает мощный инструмент, используя который можно косвенным методом ответить на ряд очень сложных и важных вопросов.

Одно то, что теория обладает суперсимметрией, позволяет даже без понимания всех тонкостей теории накладывать существенные ограничения на ее допустимые свойства. Приведем пример из лингвистики. Пусть известно, что в некоторой последовательности букв буква «у» встречается ровно три раза, и задача состоит в том, чтобы угадать эту последовательность. Не имея дополнительной информации, невозможно найти однозначное решение: подойдет любая последовательность с тремя буквами «у», например mvcfojziyxidqfqzyycdi и т. п. Но теперь допустим, что нам последовательно дают две подсказки: во-первых, ответ должен быть существующим английским словом, и, во-вторых, это слово должно содержать минимальное количество букв. Бесконечное количество первоначальных вариантов сокращается этими двумя подсказками сразу до одного кратчайшего английского слова с тремя «у»: syzygy (сизигия).

Суперсимметрия также дает подсказки, позволяющие конкретизировать ситуацию в теориях, которым свойственны такие принципы симметрии. Чтобы понять это, представьте, что вы столкнулись с физической задачей, аналогичной только что описанной задаче из лингвистики. Внутри черного ящика находится нечто неопознанное с определенным зарядом. Заряд может быть электрическим, магнитным, или иметь иную природу; для определенности примем, что этот заряд равен трем единицам электрического заряда. Без дополнительной информации определить содержимое ящика невозможно. В нем могут находиться три частицы с зарядом 1, подобные позитронам или протонам, или четыре частицы с зарядом 1 и одна частица с зарядом -1 (например, электрон), или девять частиц с зарядом 1/3 (например, и-кварки) плюс любое число незаряженных частиц (например, фотонов) и т. д. Подходит любая комбинация частиц с суммарным зарядом 3. Как и в лингвистической задаче, где единственным условием было наличие трех букв «у», число возможных вариантов содержимого черного ящика бесконечно.

Но теперь, как и в примере из лингвистики, предположим, что нам даны еще две подсказки: во-первых, теория, описывающая мир (а, следовательно, и содержимое черного ящика) является суперсимметричной, и, во-вторых, содержимое черного ящика должно иметь минимальную массу. Пользуясь результатами работ Е. Богомольного, Маноджа Прасада и Чарльза Соммерфилда, физики показали, что такая жесткая структура формализма (формализм суперсимметрии — аналог английского языка) и «условие минимальности» (минимальность массы с данным электрическим зарядом — аналог минимальной длины слова с данным числом букв «у») приводят к тому, что скрытое содержимое определяется однозначно. То есть требование минимальности массы содержимого черного ящика при условии, что заряд внутри него будет равен заданному, позволяет однозначно определить это содержимое. Состояния с данным значением заряда, в которых суммарная масса частиц минимальна, называют Б ПС-состояниями в честь трех открывших эти состояния ученых8).

Важность БПС-состояний состоит в том, что их свойства однозначно, легко и точно определяются без привлечения теории возмущений. Это справедливо вне зависимости от значения констант связи. Даже если константа связи струны велика, и, следовательно, подход с использованием теории возмущений неприменим, все равно можно вычислить точные параметры БПС-состояний. Эти параметры часто называют непертурбативными массами и зарядами, так как их значения вычислены вне рамок приближенного подхода по теории возмущений. Поэтому для читателя, владеющего английским языком, BPS можно расшифровать и как beyondperturbative states — состояния вне рамок теории возмущений.

БПС-свойства описывают лишь малую долю всех физических явлений в конкретной теории струн при больших константах связи, но эти состояния позволяют четко прояснить некоторые характеристики теории в области сильной связи. При выходе константы связи струны за рамки применимости теории возмущений, привязка к БПС-состояниям позволяет расширить границы нашего понимания теории. Как и знание лишь нескольких выборочных слов в иностранном языке, эти состояния могут нам помочь продвинуться довольно далеко.

Следуя Виттену, начнем с анализа одной из пяти теорий, например теории струн типа I, и предположим, что все ее девять пространственных измерений являются плоскими и несвернутыми. Такое предположение, разумеется, совершенно нереалистично, но оно делает анализ проще; случай свернутых измерений будет рассмотрен немного ниже. Примем сначала, что константа связи струны много меньше 1. В этом случае справедливы методы теории возмущений, и многие конкретные характеристики теории могут быть (и были) изучены довольно точно. Если мы будем увеличивать константу связи, но следить, чтобы она оставалась гораздо меньше 1, методы теории возмущений будут оставаться справедливыми. Однако конкретные характеристики теории несколько изменятся. Например, численные параметры рассеяния двух струн станут немного иными, так как изображенные на рис. 12.6 диаграммы с петлями при увеличении константы связи дадут большие вклады. Несмотря на эти изменения численных параметров, физическое содержание теории останется неизменным, если величина константы связи соответствует области применимости теории возмущений.

Когда значение константы связи струны типа I превысит единицу, методы теории возмущений станут неприменимыми, так что мы сфокусируем наше внимание на ограниченном наборе масс и зарядов БПС-состояний, которые мы еще будем в состоянии понять. Согласно гипотезе Виттена, подтвержденной затем в совместной работе с Джо Польчински из университета Санта Барбары, свойства теории струн типа I в области сильной связи в точности совпадут с известными свойствами теории О-гетеротической струны со слабой связью. Иными словами, если константа связи в теории струн типа I велика, конкретные массы и заряды, которые мы умеем вычислять, в точности совпадут с массами и зарядами в теории О-гетеротической струны с малой константой связи. Это явно указывает на то, что две теории струн, которые, подобно воде и льду, сначала казались совершенно разными, в действительности дуальны друг другу. При этом появляется убедительный довод в пользу того, что физические процессы в теории струн типа I для больших констант связи идентичны физическим процессам в теории О-гетеротической струны для малых констант связи. Схожие соображения наталкивают на мысль, что справедливо и обратное. Физические процессы в теории струн типа I для малых констант связи идентичны физическим процессам в теории О-гетеротической струны для больших констант связи9). Несмотря на то, что при анализе приближенными методами теории возмущений две теории струн кажутся не связанными, при изменении констант связи происходит переход одной из них в другую, подобный взаимным превращениям воды и льда.

Этот существенно новый результат — возможность описания физических свойств одной теории в области сильной связи в рамках другой теории в области слабой связи — называют дуальностью сильной и слабой связи. Как и рассмотренные выше примеры дуальности, эта дуальность показывает, что две теории на самом деле не являются разными. Точнее, они дают различные описания одной и той же лежащей в их основе теории. В отличие от «тривиальной» дуальности английского и китайского языков, дуальность сильной и слабой связи дает мощный инструмент исследования теорий. Если константа связи в одной из двух теорий мала, можно анализировать физические свойства с помощью хорошо известных приемов теории возмущений. Однако если константа связи велика, и теория возмущений неприменима, можно перейти к дуальной теории и вернуться к методам теории возмущений. Переход позволяет использовать количественные методы применительно к ситуациям, анализ которых, как казалось ранее, выходит за рамки наших возможностей.

Строгое доказательство того, что физические процессы в теории струн типа I для малых констант связи идентичны физическим процессам в теории О-гетеротической струны для больших констант связи и обратно, является очень сложной и до сих пор не решенной задачей. Одна из двух предположительно дуальных теорий не может быть исследована по теории возмущений, так как ее константа связи слишком велика. Это не позволяет провести прямой расчет многих физических характеристик теории. И именно этим объясняется мощный потенциал предполагаемой дуальности: если гипотеза дуальности верна, она дает новый инструмент исследования теории в области сильной связи. Нужно лишь использовать теорию возмущений для дуальной теории в области слабой связи.

Даже если нельзя доказать, что две теории дуальны, полное согласие результатов, которые можно получить строго, является неоспоримым свидетельством в пользу гипотезы дуальности сильной и слабой связи теории типа I и теории О-гетеротической струны. Эта гипотеза проходила проверку с использованием все более изощренных вычислительных методов, и неизменно находила свое подтверждение. Большинство теоретиков, занимающихся струнами, убеждены в справедливости гипотезы дуальности.

Тем же самым методом можно изучить свойства других теорий струн, например, типа IIВ. Согласно первоначальному предположению Халла и Таунсенда, которое затем было подтверждено исследованиями ряда физиков, в этой теории происходит нечто столь же необычное. При увеличении константы связи те физические свойства, которые еще можно определить, начинают совпадать со свойствами той же теории струн типа ПВ в области слабой связи. Другими словами, теория струн типа ПВ является самодуальной10). Тщательный анализ показывает, что теория струн типа ПВ с константой связи, большей 1, совершенно идентична той же теории струн с константой связи, обратной изначальной (и, следовательно, меньшей 1). Ситуация аналогична рассмотренному выше стягиванию циклического измерения до планковской длины: если уменьшать значение константы связи в теории типа ПВ до значения, меньшего 1, то вследствие самодуальности мы придем к эквивалентной теории типа ПВ с константой связи, большей 1.

Итак, посмотрим, где мы находимся. К середине 1980-х гг. физики построили пять теорий суперструн. При исследовании приближенными методами теории возмущений свойства пяти теорий казались различными. Однако эти приближенные методы применимы лишь тогда, когда константа связи струны меньше 1. Ожидалось, что константу связи в каждой теории можно будет вычислить точно, но из вида приближенных уравнений для констант стало ясно, что такое вычисление в настоящее время невозможно. Поэтому физики направили свои усилия на изучение всех пяти теорий в допустимых диапазонах соответствующих констант связи, как для констант, меньших 1, так и больших 1, т.е. при слабой и при сильной связи. Однако попытки определить свойства любой из этих теорий в области сильной связи на основе традиционных методов теории возмущений оказались тщетными.

В настоящее время физики научились рассчитывать определенные характеристики каждой теории струн в области сильной связи, используя мощный формализм суперсимметрии. Ко всеобщему изумлению всех теоретиков, свойства теории О-гетеротических струн в области сильной связи оказались идентичными свойствам теории струн типа 1 в области слабой связи, и наоборот. Более того, свойства теории струн типа IIВ в области сильной связи оказались идентичными свойствам той же теории в области слабой связи. Эти неожиданные открытия побуждают нас, следуя Виттену, перейти к анализу двух оставшихся теорий струн, струн типа IIА и Е-гетеротической струны, и выяснить, как эти теории вписываются в общую картину. И здесь нас ожидают еще более удивительные неожиданности. Для того чтобы подготовиться к ним, необходимо совершить краткий исторический экскурс.

Супергравитация

В конце 1970-х — начале 1980-х гг., до всплеска бурного интереса к теории струн, многие физики-теоретики пытались объединить квантовую теорию, гравитацию и другие взаимодействия в формализме единой теории поля для точечных частиц. Они надеялись, что препятствия, возникающие при попытках объединить теории точечных частиц, включающие квантовую механику и гравитацию, будут устранены при исследовании теорий с высокой степенью симметрии. В 1976 г. сотрудники Нью-йоркского университета Стони Брук Дэниел Фридман, Серджо Феррара и Питер ван Ньювенхейзен обнаружили, что наиболее многообещающими являются теории на основе суперсимметрии, так как в них сокращения многих квантовых флуктуаций бозонов и фермионов помогают умиротворить хаос на микроскопических масштабах. В своей работе эти ученые дали название супергравитация суперсимметричным квантовым теориям, которые разрабатывались с целью включить общую теорию относительности в единый формализм. Попытки разработать такие теории не увенчались успехом. Тем не менее, как отмечено в главе 8, урок, предвосхитивший развитие теории струн, не прошел даром.

Урок, смысл которого, вероятно, стал более ясен после работы сотрудников Парижской высшей технической школы Юджина Креммера, Бернара Джулиа и Шерка (1978 г.) состоял в том, что успешнее остальных оказались попытки построить теории супергравитации не в четырех, а в большем числе измерений. А именно, наиболее перспективными оказались варианты теорий в десяти или одиннадцати измерениях, при этом число одиннадцать оказалось максимально возможным числом измерений11). Связь с четырьмя наблюдаемыми измерениями в этих теориях также обеспечивалась путем использования формализма Калуцы-Клейна: лишние измерения сворачивались. В десятимерных теориях, как и в теории струн, сворачивалось шесть измерений, а в 11-мерной теории сворачивалось семь измерений.

Когда в 1984 г. теория струн увлекла многих физиков, виды на будущее у теорий супергравитации для точечных частиц резко ухудшились. Как уже неоднократно подчеркивалось, при точности, доступной сегодня и в обозримом будущем, струны выглядят, как точечные частицы. Это неформальное замечание можно сформулировать и в строгой форме: при изучении низкоэнергетических процессов в теории струн, т. е. процессов, в которых энергии недостаточно велики для того, чтобы прощупать протяженную ультрамикроскопическую структуру струны, можно аппроксимировать струну бесструктурной точечной частицей в формализме квантовой теории поля. Для процессов на малых расстояниях или процессов при больших энергиях такое приближение не подходит, так как мы знаем, что протяженность струны является важнейшим свойством, позволяющим разрешить конфликты между общей теорией относительности и квантовой теорией, которые теория точечных частиц разрешить не в состоянии. Однако при достаточно низких энергиях или на достаточно больших расстояниях эти проблемы не возникают, и такое приближение часто делается для удобства вычислений.

Примечательно, что квантовой теорией поля, дающей наилучшее приближение теории струн в указанном смысле, является десятимерная теория супергравитации. Особые свойства этой теории, обнаруженные в 1970-х и 1980-х гг., теперь находят свое объяснение: они являются низкоэнергетическими отголосками свойств теории струн. Исследователи, изучавшие десятимерную супергравитацию, обнаружили лишь вершину огромного айсберга конструкции теории суперструн. В действительности оказывается, что существуют четыре различных теории десятимерной супергравитации, и эти теории отличаются в деталях конкретной реализации суперсимметрии. Три из них являются низкоэнергетическими приближениями струн типа ПА, типа ИВ и Е-гетеротических струн точечными частицами. Четвертая теория является низкоэнергетическим пределом как струн типа I, так и О-гетеротических струн; в ретроспективе, этот факт был первым указанием на близость двух последних теорий.

Схема выглядит безупречной, вот только 11-мерная супергравитация осталась не у дел. В теории струн, которая формулируется в десяти измерениях, кажется, нет места для 11-мерной теории. На протяжении нескольких лет большинство физиков за редким исключением рассматривали 11-мерную супергравитацию в качестве математического курьеза, не имеющего никакого отношения к физике теории струн12).

Сегодня точка зрения радикально изменилась. На конференции «Струны-95» Виттен сделал следующее утверждение: если взять теорию струн типа IIА с константой связи, много меньшей 1, и увеличивать константу связи до значения, много большего 1, то физические свойства, которые мы еще способны анализировать (по существу, свойства насыщенных БПС-состояний), в низкоэнергетическом пределе будут соответствовать свойствам 11-мерной супергравитации.

Когда Виттен объявил о своем открытии, все присутствовавшие в аудитории потеряли дар речи, а позже весть об этом открытии громом пронеслась по всем институтам, где занимаются теорией струн. Почти для всех специалистов в этой области результат был полной неожиданностью. Первая реакция читателя этой книги, возможно, тоже будет напоминать реакцию большинства экспертов: какое отношение может иметь теория, характерная для одиннадцати измерений, к другой теории в десяти измерениях?

Ответ несет в себе глубокий смысл. Чтобы понять его, нужно описать результат Виттена более точно. На самом деле, сначала проще обратиться к другому тесно связанному с этим результату, полученному чуть позже Виттеном и стажером Принстонского университета Петром Хофавой для теории Е-гетеротической струны. Для этой теории в области сильной связи ими также было найдено описание в терминах 11-мерной теории; это поясняется на рис. 12.7. Слева на этом рисунке схематически показана теория Е-гетеротической струны с константой связи, много меньшей 1. Эта область констант связи рассматривалась в предыдущих главах и изучалась теоретиками на протяжении более десяти лет. При переходе вправо на рис. 12.7 значение константы связи постепенно увеличивается. До 1995 г. теоретикам было известно, что при этом вклады петлевых диаграмм (см. рис. 12.6) будут становиться все более важными, и при дальнейшем увеличении константы связи весь формализм теории возмущений перестает быть справедливым. Но никто не мог даже вообразить того, что при увеличении константы связи проявится новое измерение! На рис. 12.7 это измерение соответствует вертикали. Нужно помнить, что двумерная сетка на рисунке, с которого мы начали обсуждение, представляет все девять пространственных измерений Е-гетеротической струны. Новое измерение по вертикали будет десятым пространственным, так что вместе с временным измерением в сумме получается одиннадцать пространственно-временных измерений.

Рис. 12.7. При увеличении константы связи Е-гетеротической струны появляется новое измерение, и сама струна вытягивается, принимая вид цилиндрической мембраны.

Кроме того, на рис. 12.7 иллюстрируется важнейшее следствие существования этого нового измерения. Структура Е-гетеротической струны меняется по мере роста этого измерения. При увеличении константы связи из одномерной петли она растягивается в ленту, а затем — в деформированный цилиндр! Другими словами, Е-гетеротическая струна становится двумерной мембраной, ширина которой (протяженность по вертикали на рис. 12.7) определяется значением константы связи. Более десятилетия теоретики всегда использовали методы теории возмущений, основанные на предположении малости константы связи. Как показал Виттен, в этом предположении фундаментальные объекты микромира выглядят и ведут себя подобно струнам, даже если у них имеется скрытое второе пространственное измерение. Если отказаться от предположения о малости константы связи и рассмотреть физические характеристики Е-гетеротической струны при больших константах связи, второе измерение станет явным.

Это утверждение не обесценивает ни одного из выводов предыдущих глав, но побуждает рассмотреть их в рамках нового формализма. Возникает, например, вопрос, как можно состыковать новые результаты с тем, что в теории струн требуется одно временное и девять пространственных измерений? Что же, как обсуждалось в главе 8, это ограничение возникает при расчете числа различных направлений, в которых может колебаться струна, и число измерений выбирается так, чтобы квантово-механические вероятности гарантированно имели осмысленные значения. Новое измерение не является измерением, в котором может колебаться Е-гетеротическая струна, так как оно зафиксировано в самой структуре «струны». Кроме того, в формализме теории возмущений, который использовался физиками для вывода ограничения на число пространственно-временных измерений, предполагалась, что константа связи Е-гетеротической струны мала. И хотя это было осознано гораздо позднее, в таком предположении неявно используются два взаимосогласованных приближения: малая ширина мембраны на рис. 12.7, при которой она выглядит, как струна, и малый размер одиннадцатого измерения, не влияющий на вид уравнений теории возмущений. В рамках этой приближенной схемы мы вынуждены представлять себе Вселенную десятимерной и заполненной одномерными струнами. Теперь мы видим, что она 11-мерная и заполнена двумерными мембранами.

По техническим причинам, впервые Виттен столкнулся с одиннадцатым измерением при исследовании сильной связи струны типа ПА, для которой ситуация вполне аналогична. Как и в случае Е-гетеротической струны, размер одиннадцатого измерения в случае струны типа ПА определяется значением ее константы связи. При увеличении этого значения новое измерение расширяется. По мере расширения, однако, струна типа ПА превращается в «велосипедную камеру» (см. рис. 12.8), а не в ленту, как в случае Е-гетеротической струны.

Рис. 12.8. По мере увеличения константы связи для струны типа НА струны расширяются, превращаясь из одномерных петель в двумерные объекты, похожие на велосипедную камеру.

И снова, согласно Виттену, традиционные представления физиков о струнах типа IIА как об одномерных объектах, имеющих длину, но не имеющих толщины, есть следствие использования ими формализма теории возмущений, в котором константа связи струны предполагается малой. Если законы природы требуют, чтобы константа связи действительно была малой, то это приближение оправдано. Однако результаты Виттена и других физиков, полученные в ходе второй революции в теории суперструн, убедительно свидетельствуют о том, что «струны» типа ПА и Е-гетеротические «струны» имеют фундаментальную структуру двумерных мембран, живущих в 11-мерной вселенной.

Но что представляет собой 11-мерная теория? Согласно Виттену и другим исследователям, при низких (по сравнению с планковской) энергиях она аппроксимируется почти позабытой всеми 11-мерной квантово-полевой теорией супергравитации. А как же тогда описать эту теорию при высоких энергиях? Сейчас этот вопрос тщательно исследуется. Как показано на рис. 12.7 и 12.8, в такой 11-мерной теории существуют двумерные протяженные объекты — двумерные мембраны. Как мы вскоре увидим, важную роль играют и протяженные объекты других размерностей. Однако об этой 11-мерной теории ничего не известно, кроме набора разнородных фактов. Являются ли мембраны ее фундаментальными объектами? Каковы ее определяющие свойства? Благодаря каким ее свойствам она может быть связана со знакомой нам физикой? Если соответствующие константы связи малы, то лучшие ответы, которые можно дать сейчас, уже описаны в предыдущих главах, так как при малых константах связи мы возвращаемся обратно к теории струн. Но для больших констант связи в настоящее время ответов не знает никто.

Для этой II-мерной теории, что бы она собой ни представляла, Виттен придумал рабочее название: М-теория. Все расшифровывают это название по-разному. Вот примеры: мистическая теория, материнская теория («мать всех теорий»), мембранная теория (так как мембраны в любом случае играют в ней роль), матричная теория (после недавних работ Тома Бэнкса из университета Ратгерса, Вилли Фишлера из Техасского университета в Остине, Стивена Шенкера из университета Ратгерса, Сасскинда и других, предложивших новую интерпретацию теории). Однако и без точной расшифровки названия или знания ее свойств уже сейчас ясно, что М-теория дает основу для объединения всех пяти теорий струн.

Есть старая притча о трех слепцах и слоне. Первый слепец ощупывает бивень слона и говорит, что чувствует что-то гладкое и твердое. Второй держится за ногу и описывает что-то шероховатое и мускулистое. Третий слепец держит слона за хвост и говорит о чем-то гибком и хилом. Слыша описания других слепцов, каждый из них думает, что держится за другое животное. Много лет физики были столь же слепы и думали, что разные теории струн действительно являются разными. Но теперь, благодаря второй революции в теории суперструн, наступило прозрение, и они поняли, что все пять теорий струн являются частями тела одного огромного «слона» — М-теории.

В этой главе мы обсудили, как изменилось наше понимание теории струн при выходе за рамки теории возмущений, неявно использовавшейся в предыдущих главах. На рис. 12.9 подведен итог тем взаимосвязям, которые обсуждались до этого момента. Стрелками на этом рисунке обозначены дуальные теории. Видно, что мы имеем паутину взаимосвязей, но она соткана еще не полностью.

Рис. 12.10. С учетом дуальностей, включающих геометрию пространства-времени (как в главе 10) все пять теорий вместе с М-теорией связываются воедино паутиной дуальностей.

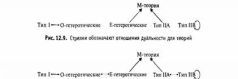Включая дуальности из главы 10, можно довести дело до конца. Вспомним о дуальности, возникающей при замене радиуса циклического измерения R на радиус 1/jR. Выше мы слегка сгладили один аспект этой дуальности, но теперь его нужно рассмотреть подробнее. В главе 10 обсуждались свойства струн во вселенной с одним циклическим измерением; при этом не указывалось конкретно, с какой из пяти теорий струн мы работаем. Как утверждалось, взаимная замена колебательных мод струны на топологические позволяет переформулировать описание (в рамках теории струн) вселенной с циклическим измерением радиуса 1/jR в терминах вселенной с циклическим измерением радиуса R. Факт, который был нами опущен, состоит в том, что теории струн типов ПА и ПВ, а также теории Е— и О-гетеротических струн в действительности не переходят сами в себя, а меняются местами при замене радиусов. Поэтому применительно к этим теориям точная формулировка дуальности при замене радиусов такова: законы физики в теории струн типа ПА во вселенной с циклическим измерением радиуса R идентичны законам физики в теории струн ПВ во вселенной с циклическим измерением радиуса 1/R. Аналогичное утверждение справедливо для теорий Е-и О-гетеротических струн. На выводах главы 10 такая формулировка не отражалась, но в данном обсуждении она играет важную роль.

Дело в том, что с учетом дуальности при замене радиусов в теориях струн типов IIА и II В, а также с учетом той же дуальности для теорий О— и Е-гетеротических струн можно достроить до конца паутину взаимосвязей, как показано на рис. 12.10 пунктирными линиями. Видно, что все пять теорий, а также М-теория, дуальны друг другу. Все они скреплены в единую теоретическую конструкцию и дают пять разных подходов для описания одной и той же физики, лежащей в основе этой формулировки. Для различных приложений может быть более удобным язык той или иной теории. Например, с теорией О-гетеротических струн в случае слабой связи работать гораздо удобнее, чем с теорией струн типа I в случае сильной связи. Тем не менее эти теории описывают одни и те же физические явления.

Теперь становятся более понятными рис. 12.1 и 12.2, приведенные в начале этой главы для иллюстрации важнейших черт теории. Как видно из рис. 12.1, до 1995 г., в отсутствие каких-либо сведений о дуальности, было пять не связанных между собой теорий. Над каждой из них работало много физиков, но без привлечения аргументов о дуальных свойствах эти теории казались различными.

У каждой теории был свой набор характеристик: своя константа связи, геометрическая структура, радиусы свернутых измерений и т.д. Физики надеялись (и продолжают надеяться) на то, что фундаментальные свойства должны определяться в рамках самой теории. Однако, не имея возможности определить их при помощи известных приближенных уравнений, теоретики, естественно, начали исследовать физические свойства во всех возможных диапазонах. Это показано на рис. 12.1, где каждая точка затушеванной области соответствует конкретному выбору константы связи и геометрии свернутых измерений. Без учета дуальности при этом все равно оставалось пять несвязанных (наборов) теорий.

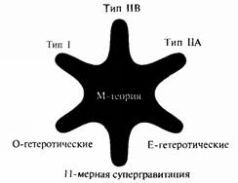
Но сейчас, когда рассмотренные выше дуальности учтены, при изменении констант связи и геометрии можно переходить от одной теории к другой, если при этом включить в анализ и объединяющую их центральную область — М-теорию (рис. 12.2). И хотя наши познания в области М-теории очень скудны, приведенные косвенные соображения дают веские аргументы в пользу того, что М-теория является основой объединения пяти на первый взгляд различных теорий струн. Более того, выясняется, что М-теория тесно связана с шестой теорией — 11-мерной супергравитацией. Это отражено на рис. 12.11, более точном варианте рис. 12.213).

Как показано на рис. 12.11, несмотря на то, что сегодня фундаментальные идеи и уравнения М-теории еще мало исследованы, они объединяют все формулировки теории струн.

Рис. 12.11. С учетом дуальностей все пять теорий струн, 11-мерная супергравитация и М-теория сливаются вместе в единую схему.

Могущественная М-теория указала физикам дорогу к новой и гораздо более глубокой единой формулировке.

Когда на территории одного из пяти полуостровов на теоретической карте рис. 12.11 константа связи струны мала, фундаментальный объект в этой теории выглядит как одномерная струна. Сейчас, однако, у нас появилась новая точка зрения. Если начать двигаться из области Е-гетеротических струн или струн типа НА, увеличивая значения соответствующих констант связи, то постепенно мы сместимся к центру карты рис. 12.11, и объекты, казавшиеся одномерными струнами, начнут вытягиваться, превращаясь в двумерные мембраны. Более того, в результате более сложной последовательности преобразований дуальности, включающих как изменения констант связи струн, так и изменения вида свернутых измерений, можно беспрепятственно перейти из любой точки на рис. 12.11 к любой другой ее точке. А так как двумерные мембраны, которые мы открыли, рассматривая Е-гетеротические струны и струны типа ПА, нам будут сопутствовать при переходе к любой из трех других формулировок, мы приходим к выводу, что двумерные мембраны на самом деле присущи любой из пяти формулировок теорий струн.

Возникают два вопроса. Во-первых, являются ли двумерные мембраны подлинно фундаментальными объектами теории струн? Во-вторых, если вспомнить о смелом рывке от нульмерных точечных частиц к одномерным струнам в 1970-х и начале 1980-х гг. и учесть только что обсужденные результаты о существовании двумерных мембран в теории струн, возможно ли, что в теории присутствуют объекты старших размерностей? На момент написания этой книги точные ответы еще не известны, но ситуация, похоже, следующая.

Чтобы разобраться в каждой из формулировок теории струн, не прибегая к теории возмущений, теоретики во многом опирались на принципы суперсимметрии. В частности, характеристики БПС-состояний, массы и заряды частиц в этих состояниях, однозначно определяются суперсимметрией, и это позволило понять некоторые свойства теории в области сильной связи без необходимости проведения прямых вычислений невообразимой сложности. На самом деле, благодаря пионерским работам Хоровица и Строминджера, а также последующей замечательной работе Польчински, о БПС-состояниях мы знаем даже больше. В частности, нам не только известны их заряды и массы, но имеется ясное представление о том, как эти состояния выглядят. И последнее, возможно, самое удивительное. Некоторые из БПС-состояний — одномерные струны. Другие представляют собой двумерные мембраны. Пока все действующие лица знакомы. И вот — сюрприз: некоторые состояния трехмерны, четырехмерны,… На самом деле диапазон возможных пространственных размерностей включает все значения до девяти включительно. Теория струн или теория, которую сейчас называют М-теорией (какое бы окончательное название ей ни дали), в действительности содержит протяженные объекты целого ряда пространственных измерений. Протяженные трехмерные объекты физики назвали 3-бранами, протяженные четырехмерные — 4-бранами, и так далее до 9-бран (в общем случае для протяженного объекта, имеющего р пространственных измерений, физики придумали не очень благозвучный термин р-брана). Иногда, используя эту терминологию, струны называют 1-бранами, а мембраны — 2-бранами. Тот факт, что все эти протяженные объекты являются равноправными объектами теории, побудил Пола Таунсенда провозгласить «демократию бран».

Несмотря на «демократию бран», струны, т.е. протяженные одномерные объекты, все-таки уникальны по следующей причине. Физики показали, что массы протяженных объектов любой размерности, кроме одномерных струн, обратно пропорциональны значению соответствующей константы связи струны, если мы работаем в рамках любой из пяти теорий струн на рис. 12.11. Это означает, что в пределе слабой связи во всех пяти формулировках все объекты, кроме струн, будут иметь огромные массы, на порядки превышающие планковскую. Поэтому из формулы Е = тс2 следует, что для их рождения потребуются огромные энергии, и они будут оказывать ничтожное влияние на законы физики (но не на все, как будет показано в следующей главе). Однако если двигаться вглубь от полуостровных областей на рис. 12.11, то браны старших размерностей станут легче, и будут играть все более важную роль14).

Таким образом, следует представлять себе такую картину: в центральной области на рис. 12.11 фундаментальными объектами теории являются не только струны и мембраны, а «браны» различных размерностей, и все они более или менее равноправны. Сейчас у нас нет ясного понимания многих свойств этой богатой теории. Одно мы знаем твердо: при движении от центральной области в сторону любого из полуостровов только струны или свернутые мембраны в обличье струн (рис. 12.7 и 12.8) оказываются достаточно легкими, чтобы сохраниться и привести к известной нам физике — частицам из табл. 1.1 и четырем типам взаимодействий. Подход теории возмущений, который физики использовали почти два десятилетия, был недостаточно гибок для того, чтобы выявить существование протяженных объектов огромной массы и других размерностей. Центральным объектом анализа были струны, и теория получила далеко не демократическое название теории струн. Отметим еще раз, что в этих областях рис. 12.11 для большинства исследований можно с полным основанием пренебречь всеми объектами, кроме струн. По существу, в предыдущих главах этой книги мы так и поступали. Однако сейчас мы видим, что теория оказалась в действительности богаче, чем кто-либо ранее предполагал.

И да, и нет. Нам удалось достичь более глубокого понимания, освободившись от некоторых выводов, которые, как стало ясно теперь, были следствиями использования теории возмущений, а не истинных принципов теории струн. Однако в настоящее время методы, позволяющие работать вне рамок теории возмущений, весьма ограничены. Открытие замечательной системы дуальных связей позволяет глубже постичь теорию струн, но многие вопросы остаются неразрешенными. Например, мы еще не знаем, как выйти за рамки приближенных уравнений для определения значения константы связи струны. Как обсуждалось выше, эти уравнения слишком грубые, чтобы из них можно было извлечь хоть какую-то полезную информацию. Нет у нас и существенных продвижений по вопросам о том, почему протяженных пространственных измерений именно три или каким должен быть точный вид многообразия для свернутых измерений. Для ответа на эти вопросы нужны более отточенные инструменты исследований вне рамок теории возмущений, чем те, которыми мы сегодня обладаем.

То, что действительно появилось, — это гораздо более глубокое понимание логической структуры и исследовательского диапазона теории струн. До открытий, итог которым подведен на рис. 12.11, поведение каждой теории струн в области сильной связи было полной загадкой. Как на средневековых картах, царство сильной связи было белым пятном, на которое, сообразно фантазии картографа, наносились изображения драконов и морских чудовищ. Но сейчас мы видим, что хотя путешествие в это царство может завести нас в неизведанные просторы М-теории, в конце концов мы снова выйдем в курортную зону слабой связи, где говорят на дуальном языке другой теории струн, ранее считавшейся совершенно непохожей.

Дуальность и М-теория объединяют пять теорий струн, подталкивая к важному выводу. Может оказаться и так, что нас больше не поджидают удивительные открытия, сравнимые с описанными выше. Как только картограф обозначил все точки на глобусе Земли, глобус готов, и география исчерпана. Это не означает, что разведка местности в Антарктиде или на необитаемых островах в Микронезии лишены всякой научной или культурной ценности. Это означает лишь, что век географических открытий подошел к концу. И свидетельством тому — отсутствие белых пятен на карте. «Теоретическая карта» на рис. 12.11 имеет для теоретиков, занимающихся струнами, такое же значение. Она покрывает все сферы теории, в которые можно попасть, отправляясь из области любой из пяти формулировок струн. И хотя нам далеко до полного понимания неизведанной М-теории, на карте нет белых пятен. Как и картограф, теоретик может теперь со сдержанным оптимизмом заявить, что весь спектр логически обоснованных теорий, вбирающих в себя все важные открытия прошлого века — специальную и общую теории относительности, квантовую механику, калибровочные теории сильного, слабого и электромагнитного взаимодействий, суперсимметрию, дополнительные измерения Калуцы и Клейна, — уже нанесен на карту рис. 12.11.

Задача струнного теоретика (возможно, его уже нужно называть М-теоретиком) — показать, что некая точка на теоретической карте рис. 12.11 действительно описывает нашу Вселенную. Чтобы осуществить это, нужно найти исчерпывающие и точные уравнения, решения которых позволили бы поймать эту неуловимую точку на карте, а затем добиться понимания соответствующих физических явлений, достаточного для сравнения с экспериментом. По словам Вит-тена, «понимание того, чем в действительности является М-теория, т. е. какую физику она несет в себе, повлияет на наше понимание природы не менее сильно, чем любое из главных научных потрясений прошлого»15). В этом суть программы построения объединенной теории в XXI в