"Математика, Философия и Йога" - читать интересную книгу автора (Меррелл-Вольф Франклин)

Лекция 4

Сегодня мы рассмотрим несколько различных вопросов V-/- фрагментов, часть которых станет подготовкой к завершающей лекции. Но прежде я хотел бы поговорить об одном очень важном переживании, которое может возникнуть у человека. Это ощущение Нумена. Сначала я использую вместо ранее начерченной линии другой рисунок, который поможет изобразить границу между тем сознанием вверху, которое лишено дискретности и является непрерывным потоком, и обычным, двойственным сознанием внизу. Нарисуем вместо этой черты храм, открытый внешний двор которого изобразим в нижней части рисунка, то есть в высших областях двойственного сознания (см. рис. 13).

Рис.13

Вот непроницаемая стена, в ней дверь, и я даже не пытаюсь описать внутренние помещения этого храма. Открытый двор перед дверьми олицетворяет высшие возможности, которых может достичь неозаренный разум, – и редкий разум способен подняться в эту область. Для этого ему нужно быть одновременно и утонченным, и мощным. В сфере двойственного сознания нет такой силы, которая смогла бы взломать врата храма. Помните об этом: взять эту дверь приступом не может никакая сила, кроме одной: полного смирения. Впрочем, такой способ нельзя назвать применением силы – скорее это мольба. Претендент, поднявшийся столь высоко благодаря способностям своего разума (есть и другие пути, но сейчас я веду речь только об этом), неизбежно сталкивается с необходимостью полностью пожертвовать всем, чем он владеет, достичь настоящего, а не напускного смирения. В данном случае прежде всего следует принести в жертву интеллектуальную гордыню. Для такого претендента это единственная возможность. У того, кто явился сюда, есть и иной выбор: пасть жертвой асурического соблазна, то есть комплекса власти. Тот, кто пытается воспользоваться низшей властью, чтобы повелевать тем, что выше него, избирает асурический путь, а на этом пути человека рано или поздно ожидает гибель души. Это совсем не пустяк. Нет ничего, ничего страшнее, перед этим бледнеет даже атомная бомба, так как она не влечет гибели души. Предположим, однако, что человеку удается подобрать к дверям ключ – ключ смирения и полного жертвоприношения; тогда он входит в храм и здесь его ждут такие переживания, которые совершенно невозможно уместить в рамки логического разума.

Оставим пока этот символ и поговорим о доступных рассуждениям обстоятельствах встречи с Нуменом. Когда-то мне в руки попала книга под названием «Озари мягким светом» [1]. Ее автор встретил Махатму Ганди; он был восхищен этим человек и стал, по собственному утверждению, его челой. Он оказался свидетелем убийства Ганди; к тому времени он настолько отождествился с учителем, что, по его собственным словам, ощутил пулю так, словно она пронзила его самого. В этой книге или, возможно, в статье того же автора я впервые встретил имя Шри Ауробиндо. Автор рассказывал об одном наблюдении, которое поразило его до глубины души. Он посетил ашрам Ауробиндо во время одного из крупнейших даршанов [2], проводимых четыре раза в год; в это время Ауробиндо и Мать [3] устраивали открытые встречи с учениками и всеми желающими. Собиралось множество людей – некоторые, как и сам автор книги, не имели четко определенной приверженности и просто хотели узнать, что там происходит. Автор был воспитан в католической атмосфере, и его изумило, что некоторые люди – не только индийцы, но и европейцы и американцы – падали на колени и простирались у ног Шри Ауробиндо. Прежде автор видел такое перед глиняными идолами и отнесся к этому спокойно, но теперь он был глубоко поражен тем, что люди падают ниц перед обычным земным человеком.

Я рассказываю об этом для того, чтобы вы не испытывали ни удивления, ни презрения, если станете свидетелем подобной сцены. Ауробиндо никогда не требовал этого. Однажды его спросили, как он это расценивает, и он сказал: «Каждый может здороваться со мной как захочет». Вы могли поклониться, могли сложить ладони вместе (этот жест означает: «Я приветствую Божественное в тебе»), могли опуститься на колени и даже лечь на пол. Для Ауробиндо это было неважно, но он говорил: «Те, кто решается на такой шаг, ощущают нечто не только разумом, но и всем телом, и потому им разрешается так поступать».

Одни могут практиковать коленопреклоненное или распростертое положение как знак почтительности и благоговения, но другие принимают его совершенно спонтанно, они не в силах противиться порыву, потому что ощущают присутствие Нумена. Истиной остается то, что в этом мире есть люди, которые на вид кажутся обычными земными людьми, но при этом всегда – или изредка – являются проводниками Нумена. С другой стороны, есть и такие, кто способен осознать присутствие Нумена. Временами, хотя и не всегда, у них возникает впечатление, что стоящая перед ними человеческая фигура исчезает или преображается, а на ее месте возникает иная Фигура – она источает настолько ослепительное сияние, что человек беспомощно падает на колени. Это действительно возможно. Такое присутствие может оказаться совершенно всепоглощающим. Я повторю это еще раз: все это происходит на самом деле. При этом тот человек, который несет в себе Нумен, испытывает чувство глубочайшего смирения – ощущение того, что он просто не достоин хранить в себе подобную драгоценность. И все же необходимо разрешить самому себе такое проявление поклонения, искреннего восторга, какое возникает, когда человек вверяет себя Нумену. Здесь вы на священной, подлинно священной земле. Это переживание – одно из самых всепоглощающих чувств, которые могут возникнуть у человека. Оно может сопровождаться такими сильными ощущениями блаженства, полной правильности происходящего и восторженности, какие человек просто не в состоянии вообразить – нечто такое, для чего нет слов, потому что в наших обыденных переживаниях никогда не случается ничего достойного сравнения. Тот, кому довелось ощутить присутствие Нумена, поистине счастлив. Это чувство выходит за рамки любых описаний. Мой рассказ – только подготовка к нему. Это переживание представляет собой слияние души, Атмана, Психической Сущности в понятиях Ауробиндо – и Божественности. Пусть разум безмолвствует, потому что это подлинное благословение.

Однако сегодня вечером я должен рассказать вам о многом другом, и большая часть этого послужит нам подготовкой к тому, о чем пойдет разговор в завершающей лекции. Предстоит обсудить многое, и потому мне придется поспешить.

Итак, прежде всего, существуют понятия, привычные для нашего обычного, двойственного сознания -в идеальном случае, они допускают исчерпывающее определение, а те понятия, которые являются полностью определимыми, должны классифицироваться как математические. И все же выше этой границы (черты, впервые проведенной на рисунке 1 и вновь изображенной на рисунке 14) есть некая область, проникнув в которую очищенный разум получает возможность доступа к иного рода понятиям.

Неопределимое Определимое- Неопределимое

Определимое

Рис.14

Эту область можно назвать «определимое-неопределимое». Будучи определимым, она может использоваться разумом для передачи мыслей, но в своих неопределимых глубинах смыкается с бесконечностью. Эти глубины невозможно передать обычными словами. Для того чтобы они стали хоть в малой мере понятными, необходимо прибегнуть к чему-то такому, что относится к интуиции. По этой причине их целью не является некая философская система. Скорее это сосуды, которые могут вмещать в себя некую сущность, – то, что персидские мистики часто символически называли вином. Эти понятия могут быть носителями, хранилищами. Важным становится не само понятие, а то, что оно в себе несет.

Одни понятия оказываются лучше других, однако существует огромный диапазон возможных случаев, и для того, чтобы показать это, я воспользуюсь примером великого европейского мистика Якоба Бёме [4]. Фон Гартманн [5] считал его не просто великим, а величайшим; и хотя нельзя утверждать, что его этическое ощущение или, если хотите, этический покров опустился на квакеров (или Общества Друзей) в целом, но именно духовный призыв Якоба Бёме вызвал к жизни труды Джорджа Фокса, основателя первой квакерской общины.

Его вдохновенная мысль стала важным вкладом в работы немецких философов-идеалистов, несмотря на то что сам Бёме никогда не писал на языке философии. Вообще говоря, в те времена язык немецкой философии еще не возник. Бёме был высокообразованным человеком и испытал невероятно глубокие переживания. Мне кажется, что в поисках подходящего языка для наиболее вразумительного разъяснения он выбрал самый неудачный – язык алхимиков [6]. Дело в том, что алхимики имели привычку объяснять туманное содержание еще более туманными понятиями. В результате при попытке прочесть Якоба Бёме хочется рвать на себе волосы. Тем не менее известен пример одного шотландца и его жены, которые старательно прочли труды Бёме. Они признавались, что не поняли ни единого слова, но это чтение принесло им огромную пользу. Я говорю именно об этом: они уловили суть, несмотря на то что не могли понять ни одного термина.

Я тоже не склонен пользоваться языком алхимии и предпочитаю язык математики – мне он представляется намного более ясным. Однако не забывайте, что решающее значение имеют не внешние формы понятий, слов и предложений, а кроющееся в них содержание. В этом заключается способ использования письменных знаков для передачи вложенного в них свыше смысла.

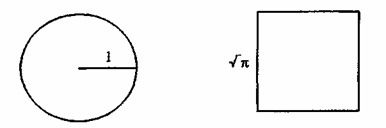
Сегодня я собираюсь поговорить об одном чрезвычайно важном числе. Его важность измеряется не только практическим, но и религиозным значением. Это число известно нам как я. Судя по всему, Великая Пирамида – настоящий памятник этому числу. То есть это очень старое число, оно было известно уже в древности. В те времена оно играло важную роль в посвящениях.

КВАДРАТУРА КРУГА

Рис.15

Объяснить его значение в обычном математическом смысле нетрудно. Это отношение длины окружности к ее диаметру. Если бы человек мог точно вычислить это отношение, то не испытывал бы никаких затруднений с решением задачи о квадратуре круга (см. рис. 15).

В этой задаче заключен совершенно необычный смысл. Однако давайте сперва попробуем обойтись обычным здравым смыслом. А в обычном смысле эта задача заключается в построении квадрата, площадь которого в точности равна площади заданного круга. Сегодня уже известно, что если разрешается пользоваться только циркулем и линейкой, такой квадрат невозможно построить, хотя другие методы и подходы позволяют решить эту задачу. Кажется, Платон [7] настаивал на том, что единственными допустимыми инструментами должны быть циркуль и угольник. В этом случае решение невозможно – так же как и решения задач о трисекции угла и удвоении куба; однако все эти задачи могут быть теоретически решены другими методами. Итак, в обыденном смысле, когда это просто геометрическая задача, произвести квадратуру круга можно, но это никак не связано с тем более глубоким содержанием, которое интересует нас сейчас.

Что символизируют круг и квадрат? Нас волнует не геометрическая сторона, а нечто более глубокое. Мы имеем дело с символами, а не чисто математическими фигурами в обычном смысле слова. Круг олицетворяет область вне двойственного сознания. С другой стороны, будучи средством проведения измерений, квадрат означает двойственное сознание -ту сферу, где возможны измерения, определения и так далее. Любые участки земли, площади и поверхности – какие угодно – измеряются квадратами или треугольниками. В дифференциальном исчислении эти квадраты или треугольники просто делают настолько малыми, что они оказываются меньше любой имеющей название единицы меры, но сам принцип остается таким же. Мера, определение, точное понятие – все это олицетворяется квадратом. Таким образом, квадратура круга может означать попытку перенести нечто, относящееся к Трансцендентному, в рамки относительного, двойственного сознания. Иными словами, круг представляет собой царство богов, а квадрат – мир человека, или же, используя еще одно сравнение, квадрат символизирует область времени, бесконечно перемещающегося от беспредельного прошлого к неизмеримому будущему. Круг означает саму вечность – и это не просто бесконечный срок, так как подняться ко всей полноте вечности можно в одно мгновение. Это безвременье, и, по меркам обычного времени, один его миг ничем не отличается от миллионов лет, поскольку понятие времени там просто неуместно. Это то состояние, когда все происходит всегда и одновременно.

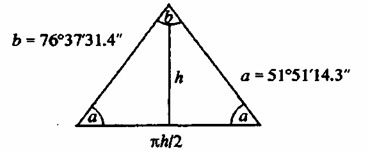
Давайте теперь посмотрим на схему Великой Пирамиды в Гизе (см. рис. 16). Я собираюсь использовать ее только в качестве примера. Всестороннее обсуждение этого памятника потребовало бы намного больше времени, чем наши шесть лекций. Я привожу этот пример, опираясь на исследования Пьяцци Смита, Королевского астронома Шотландии – то есть опытного ученого, – который знал толк в точности измерений и, что особенно важно, понимал астрономическое значение Великой Пирамиды. Это очень обширная и удивительно интересная тема. Пирамиды таят множество приковывающих внимание загадок, но я хочу поговорить только об одной из них: мы обсудим угол у основания, а. На схеме показано сечение пирамиды, проходящее через ее вершину перпендикулярно основанию. Смит обнаружил, что углы пирамиды очень трудно измерить, так как вандалы уже давно разобрали облицовочные камни (и использовали их для постройки домов в Каире), после чего склоны оказались чрезвычайно огрубленными. У оснований скопились груды разбитых камней, однако сохранившихся свидетельств было достаточно для вывода о том, что пирамида определенным образом изображает число пи.

ГЕОМЕТРИЯ ВЕЛИКОЙ ПИРАМИДЫ

Рис.16

Если угол а равен 51° 51' 14,3" › то у любой пирамиды тех же пропорций (то есть независимо от ее действительных размеров) длина вертикали h, проведенной от вершины до основания, будет равна радиусу окружности, длина которой равна периметру квадратного основания пирамиды. Хотя значения, полученные ученым при первоначальных измерениях, не согласовывались с точным соотношением, позже ему удалось найти несколько недостающих облицовочных камней, сохранившихся под грудами булыжников. Так появилось доказательство, что изначально поверхность пирамиды была не ступенчатой, как сейчас, а гладкой, покрытой облицовочными глыбами известняка (такие камни трапециевидной формы до сих пор сохранились на верхушках соседних пирамид). Благодаря этому угол а удалось измерить точнее, и он оказался именно таким, как предполагала эта теория.

Более того, тот факт, что пирамида действительно была выстроена отчасти для «увековечивания», как выражается Смит, числа пи, подтверждается также бесчисленными неявными пропорциями Царской гробницы, передней камеры и других внутренних помещений – повсюду обнаруживается одна и та же зависимость, выражающаяся с точностью до пятого знака числом 3,14159 (то есть точнее, чем общепринятое значение 3,1416). Те, кто владеет методами математических вычислений, могут попробовать использовать угол 51° 51' 14,3" и убедиться в том, что он позволяет с необходимой точностью получить число пи. Я сделал это и получил пять знаков после запятой.

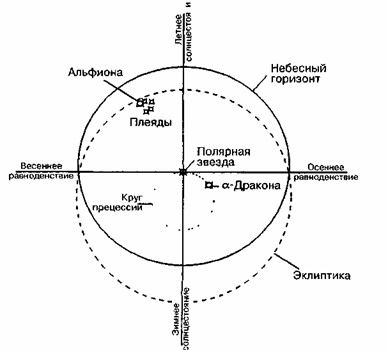
Обратимся к другим свойствам пирамиды. Вот еще один пример, на который я хочу обратить ваше внимание. Он настоятельно подталкивает нас к идее Пифагора о том, что числа направляют эволюцию, хотя сейчас не время погружаться в эту тему. Однако мне хочется рассказать кое-что о той эпохе, когда люди строили эту пирамиду (см. рис. 17). Направление коридора, ведущего от входа внутрь пирамиды, указывает на ту точку неба, где в те времена находилась звезда Альфа Дракона [8] (сейчас там находится Полярная звезда) в момент пересечения нижнего полярного меридиана, а звезда Альфиона из Плеяд-в точке весеннего равноденствия (см. рис. 18). Астрономические вычисления позволяют определить, когда Альфа Дракона находилась у небесного полюса. Конечно, она не совпадала с этим полюсом в точности, а Полярная звезда не совпадает с ним в наши дни, и все же когда-то Альфа Дракона играла ту же роль, которую сегодня играет Полярная звезда.

ВЕЛИКАЯ ПИРАМИДА В ГИЗЕ

Рис.17

ПРЕЦЕССИЯ ТОЧЕК РАВНОДЕНСТВИЯ

Рис.18

Полагаю, не все вы знакомы с понятием прецессии точек равноденствия. Дело в том, что земля движется подобно обычному волчку. Если вы когда-нибудь играли волчком, то заметили такую особенность: вначале он вращается строго вокруг своей оси, но вскоре его верхушка начинает совершает обороты, очерчивая эллипс. Кроме того, весь волчок в целом кружится в более обширной системе отсчета. Такое движение называют прецессией. Земле тоже свойственно прецессионное смещение относительно всей галактики, хотя один виток этой прецессии продолжается намного дольше человеческой жизни. Современные подсчеты (они не могут считаться очень точными, так как представляют собой долгосрочную экстраполяцию на основе измерений, которые были проведены в короткий период) позволяют оценить продолжительность одного цикла прецессии сроком в 25868 лет [9]. Между тем некоторые параметры пирамиды определяют эту продолжительность как 25827 лет -довольно близкое значение. Не исключено, что вторая оценка даже точнее современной; вполне возможно также, что это число было правильным в эпоху сооружения пирамиды, а с тех пор период прецессии изменился. Так или иначе, нам не известно, какое из двух значений точнее, но их сходство вызывает изумление.

Эти значения позволяют предположить, что коридор входа в пирамиду был точно направлен на Альфу Дракона в 2170 году до нашей эры. Большинство начинающих экзотериков тут же скажут, что этот год, вероятно, и является датой ее сооружения, но это не совсем верно. Более точный ответ звучит так: пирамида была построена в 2170+N*25868 году до нашей эры. Это действительно могло случиться в 2170 году до нашей эры, но могло быть и на двадцать шесть тысячелетий раньше, и еще на двадцать шесть тысяч лет раньше. Помните, я не указываю вам точную дату около 2000 лет назад. Вполне возможно, что это произошло две тысячи лет тому плюс несколько раз по 25868 лет. В «Тайной доктрине» [10] говорится, что число пи равно трем, а это означает примерно семьдесят восемь тысячелетий. Вы можете усомниться в том, что рукотворное сооружение способно сохраниться на протяжении такого времени. Но ведь обычные горы могут стоять такой срок. Конечно, на них возникают следы эрозии. Однако пирамиды выстроены из очень крепких блоков песчаника и имеют самую долговечную форму – форму пирамиды, у которой нет отвесных стен: ее пологие склоны нельзя разрушить толчками. Помимо того, на стенах Гробницы Царицы остались солевые отложения, позволяющие предположить, что основание сооружения некогда опустилось, а затем вновь поднялось, а соль отложилась в этом помещении в те времена, когда пирамида полностью или частично была погружена в океан. Я не выношу какого-либо определенного суждения, просто излагаю вам разнообразные варианты.

Кто построил эту пирамиду? Пьяцци Смит убежден в том, что египтяне не владели достаточными познаниями, чтобы это сделать. Нет никаких признаков того, что египтянам были доступны знания, заложенные в конструкцию пирамиды: если они и существовали, то в форме эзотерических знаний жрецов, и были запретными для экзотерических ученых и учеников. Смит пришел к выводу, что человеческий разум не был способен воздвигнуть подобное строение и потому оно возникло благодаря вмешательству Господа (Бога он понимал в теологическом смысле) и его проводников. В «Тайной доктрине» выдвигается мысль о том, что пирамида была сооружена некоей древней расой, чья страна затонула в океане задолго до Посейдониса – континента, исчезнувшего, согласно платоновскому «Тимею» [11], около десяти тысяч лет тому назад; более того, пирамида является вестью для грядущих поколений.

Если вы хотите сообщить нечто людям, которые будут жить много тысячелетий спустя, то бессмысленно использовать для этого родной язык. Необходим некий всеобщий язык, и потому у той расы не оставалось иного выбора, кроме математики – языка измерений. Кстати, я хочу выделить один вопрос: какими единицами измерения они пользовались? Маловероятно, что это был английский фут, да и вообще чья-либо стопа*. Вообще говоря, футов очень много, так как стопы правителей разных стран имеют различную длину. Скорее, использовавшаяся строителями единица измерения была сродни нашему метру, который считается близким к одной десятимиллионной части длины дуги от полюса до экватора, но в данном случае египетская мера еще утонченнее и подразумевает более глубокие познания, так как в точности равна одной десятимиллионной половины полярной оси.

Это указывает на прекрасные знания о Земле, которые позже были забыты и открыты заново лишь в последние триста лет. Они весьма впечатляют. Многие, очень многие ученые не могут смириться с этим и твердят: «Случайное совпадение!» Однако им приходится повторять эти слова так часто, что подобные совпадения становятся совершенно невероятными. Но они так неприятны… Великая Пирамида была построена отнюдь не примитивным народом, а наши теории утверждают, что в те времена жили только неразвитые человеческие существа уровня каменного века. Да, разумеется, люди каменного века тоже были. Вы когда-нибудь задумывались о том, что записи времен каменного века имеют больше шансов сохраниться, чем летописи цивилизованных народов, пользующихся металлами? Камень сохраняет надписи очень долго, а металлы ржавеют и подвергаются коррозии; что касается органических веществ, то они просто исчезают. Нет, это действительно целый переворот во взглядах, это "просто потрясает. Подобные факты опровергают нашу теорию, такую удобную теорию о том, что вплоть до нашего появления человек был совершенно глуп. Конечно, очень приятно считать себя стоящим на вершине горы и покровительственно взирать на живших в прежние эпохи. Однако именно древние построили эту гору и все, что спрятано внутри нее. Чувство удовлетворенности исчезает, а ученым это не по нраву.

Однако мы говорили о том, что если вы хотите передать какие-то сведения, то это придется делать с помощью численных измерений, а не словесных описаний. Само собой разумеется, математика является всеобщим языком. Например, пи встречается повсюду, и если вы собираетесь вступить в общение с цивилизованным народом (предположим, что такие люди существуют), что может быть лучше, чем указать число пи. Существует множество способов указать его, и будущие люди несомненно будут их знать, что станет неоспоримым свидетельством их разумности. В результате возникнет определенная форма общения посредством математики, всеобщего языка; именно это и произошло в данном случае.

В отношении назначения этой пирамиды существует традиционное мнение: она никогда не служила гробницей. Пьяцци Смит очень убедительно это показывает. Хотя в Царской гробнице действительно стоит саркофаг, он также изобилует информацией, которую можно извлечь путем измерений. Судя по всему, прочие пирамиды были подражаниями и служили гробницами -но не Великая Пирамида. Смит утверждает, что в Египте, да и вообще в мире, нет другой пирамиды с таким же углом между основанием и боковой гранью. Она уникальна и потому по традиции считается местом проведения посвящений. Я слышал, что посвящения были довольно суровыми. Претендента укладывали в саркофаг, задвигали каменную крышку, которую человек был не в силах поднять, после чего кандидату предстояло выбраться из заключения. Поскольку это было невозможно сделать физически, ему приходилось перенестись в более тонкое вместилище, а для этого – погрузиться в кататонический транс. Спустя три дня саркофаг открывали и, если человеку не удалось достичь транса, оттуда извлекали мертвое тело. Во всяком случае, так описывают посвящение сохранившиеся легенды. Я не могу поручиться за их истинность. У меня нет однозначного мнения, но это интересные истории. В них есть смысл.

Сколько подобных загадок возникло в давние эпохи, было передано египетским жрецам и сохранено ими в форме эзотерических знаний, которые, в свою очередь, были вручены Моисею – ведь мы встречаем число лив древнееврейском! Одним из важнейших слов в нем было имя Элохим. Каждая древнееврейская буква одновременно является и числом. Если заменить буквы слова Элохим числами, получится анаграмма из тех же цифр, что и число 31415. В этой записи нет десятичной точки. Цифры входят в нее в другом порядке. Это анаграмма. Но она наводит на мысли. Это чрезвычайно богатая пища для размышлений.

Какие слова в других языках обозначают то же самое, что и «Элохим» в древнееврейском? У индуистов это Кумара, у буддистов -Дхьян-Чохан. Как они определяются? Это бывшие смертные люди, которые вышли за рамки человеческой эволюции. Вы продвинетесь чуть дальше. Сделайте еще шаг и обратитесь к «Письмам махатм» [12] – существуют свидетельства, что Разумные Сущности, написавшие эти «Письма», сыграли важнейшую роль и в создании «Тайной доктрины». Сама Е. П. Б. говорила, что была писателем, а не автором, хотя это чрезмерная скромность. Она все же написала определенные главы самостоятельно, хотя большая часть книги была записана под диктовку. В одном из «Писем махатм» есть фрагмент древнего буддийского текста, и в нем встречаются ссылки на Татхагату [13]; при этом каждый раз после имени «Татхагата» в скобках фигурируют слова «Дхьян-Чохан».

Итак, поскольку число пи олицетворяет собой, так сказать, границу между квадратом и кругом, между обычным сознанием и сознанием внешним, не указывает ли оно на то, что элохимы, кумары, дхьян-чоханы, татхагаты – то есть люди настолько возвысившиеся, что встреча с ними оказалась бы намного обширнее любых возникающих у нас, любых доступных нам, простым смертным, умозрительных представлений о Боге, – пребывают на границе между Трансцендентным Там и проявленным здесь, внизу? Я предлагаю вам подумать об этом.

Число пи возникает повсюду. Оно символизирует все то, что называют трансцендентными числами – и это очень своеобразные числа. Их строгое определение звучит достаточно непонятно. Тем, у кого нет математического образования, оно, скорее всего, покажется бессмыслицей, и потому мне придется перейти к наглядным примерам. Прежде всего, каждый знает, что такое целые числа. Все мы знакомы и с дробями, которые частично заполняют промежутки между целыми. Если вы изучали алгебру, то помните, что существуют и отрицательные числа: -1, -2 и так далее. Кроме того, есть числа иррациональные – такие, как V2. Они располагаются повсюду между целыми и дробями. Помните, что те точки на прямой, которые соответствуют числам, не имеют никаких размеров, то есть их поразительно много даже в крошечном отрезке. Вообще говоря, на любом отрезке их бесконечно много, их просто невозможно сосчитать.

Однако даже эти классы не покрывают всех существующих чисел. Есть числа, которые называют «мнимыми». Одним из них является число V-1, его обычно обозначают знаком i. Это число нельзя отнести к какому-либо из перечисленных классов, и потому для изображения чисел li, 2i, 3i, 4i, дробных и иррациональных i спользуется вертикальная ось (см. рис. 19). Наконец, существуют сочетания мнимых и действительных чисел. Пусть у нас есть число 2i, отмеченное на вертикальной оси, и обычное число 3, показанное на оси горизонтальной. Отметим точку А, которая будет соответствовать числу 3 +2i. Такие величины называются комплексными. С ними можно проводить любые действия, включая обратные операции, и в результате получатся другие числа на той же двумерной плоскости. Это значит, что вы можете не только складывать такие числа, но и вычитать одно из другого – ведь в нашем распоряжении есть отрицательные величины. Можно извлечь из любого комплексного числа корень и получить иррациональное комплексное число. Использование иррациональных чисел и переход к мнимым и комплексным величинам обеспечивают все возможные сочетания и позволяют извлечь корень из любого, даже отрицательного числа. Результатом любой операции на этой плоскости станет какая-либо точка той же плоскости, и это первый случай, когда такое требование выполняется. Это полное и замкнутое числовое поле.

КОМПЛЕКСНЫЕ ЧИСЛА

Рис.19

Что касается трансцендентных чисел, то они не входят и в эту группу, то есть не могут быть обозначены на этой плоскости. Точки комплексной плоскости называют алгебраическими числами, так как они могут быть решениями алгебраических уравнений с целыми коэффициентами, а трансцендентные числа -нет. Их называют трансцендентными именно по этой, сугубо технической причине, и вполне возможно, что тот математик, который ввел это название, не до конца осознавал, что именно оно означает. Не исключено, что эти числа трансцендентны и в ином смысле.

Вот некоторые причудливые свойства трансцендентых чисел. Самыми известными и чрезвычайно важными из них являются пи и е (я надеялся, что смогу наглядно объяснить и второе число, но мне это не удалось). Некто сказал, что вселенная вообще не смогла бы существовать без пи и е; в более традиционном смысле можно утверждать, что в отсутствие пи и е нам никогда не удалось бы постичь вселенную и управлять ею. Видите, насколько важны числа? Впрочем, я не буду отклоняться от темы. Времени осталось мало, так что опустим этот вопрос.

В числе пи действительно есть нечто загадочное. Предположим, у вас есть поверхность с рядом параллельных прямых и расстояния между соседними линиями одинаковы. Возьмем несколько булавок или иголок – любые предметы подобной формы, -длина которых в точности равна расстоянию между прямыми. Бросим их на эту поверхность пятьсот, тысячу раз и подсчитаем количество булавок, которые не пересекли ни одной прямой, и число булавок, пересекших хотя бы одну линию. Будем вносить эти суммы в два столбца и вычислять отношение соседних пар чисел. Мы обнаружим, что оно приближается к числу пи/4. Откуда возникло число пи? Оно входит в формулу, эмпирическую формулу, связанную с вопросами вероятности. Какое отношение может иметь число пи, например, к задаче определения того, какой процент населения доживает до семидесяти лет? Связь существует. Число пи входит и в эту формулу. Тот факт, что это число входит в уравнения теории вероятности, позволяет уверенно предположить, что упорядоченность присуща самым случайным событиям, и даже те явления, которые выглядят совершенно непредсказуемыми, подчиняются какой-то закономерности. Эти загадки вызывают трепет. Для того чтобы понять их, нужно быть хоть немного математиком, и тогда они действительно вызовут холодок в спине. Если вы просто бросаете булавки на поверхность, никакого трепета не возникнет. Однако это и в самом деле совершенно загадочные законы.

Число пи можно получить множеством других способов. Оно определяет суммы некоторых бесконечных рядов, а также непрерывных последовательностей умножений или делений. Один из таких рядов указал Лейбниц:

π/4= 1-1/3+ 1/5-1/7 +…+ 1/(2n-1) +…

В нем плюсы и минусы перемежаются, а знаменатели дробей представляют собой последовательность нечетных целых чисел. Если вы хотите определить значение числа пи, достаточно складывать члены этого ряда до тех пор, пока не надоест. Следует заметить, что вам придется провести очень много сложений, прежде чем удастся получить точное значение двенадцатого знака после запятой. Этот ряд – не самый удачный метод вычислений, поскольку он, как говорят математики, сходится очень медленно. Есть другие, быстросходящиеся ряды, но и они тоже остаются просто бесконечными суммами и не имеют никакого сходства с закономерностью, связывающей длину окружности и ее диаметр.

Вы можете подумать, что в настоящее время мы не знаем – и не найдем в обозримом будущем -других трансцендентных чисел, кроме этих двух, что эти числа очень редкие. Однако математики уже разработали несколько бесконечных классов трансцендентных чисел, и существуют доказательства того, что их число во многом превосходит количество всех остальных чисел вместе взятых. Дело в том, что в отличие от прочих чисел, которые (теоретически) за достаточно долгое время можно пересчитать, счесть все трансцендентные числа просто невозможно. Трансцендентные величины образуют множество} i – уровень бесконечности [14], превосходящий по мощности все остальные числа, которые входят в множество}о.

Некоторые математики утверждают, что рассмотренная числовая плоскость (рис. 19) является в действительности не сплошной, а пористой, и такие «дырочки» соответствуют трансцендентным числам. Множество алгебраических чисел, всех тех, что я вам показал, является счетным. Это означает, что целых чисел вполне достаточно (внимание, перед вами настоящая тайна!) для того, чтобы сосчитать не только все целые числа, но также все дроби, иррациональные, мнимые и комплексные числа. Вот куда заводит математическая логика. Это свойство бесконечного многообразия: вы можете исключить из него бесконечное число бесконечных многообразий и при этом исходное многообразие ничуть не уменьшится [15].