"Три дня в Карликании" - читать интересную книгу автора (Левшин Владимир Артурович)

Чудесные признаки

Мы с трудом уговорили Четвёрку с бантиком пойти домой. Ей надо было отдохнуть после стольких волнений. Назначив нам час и место встречи, она убежала, а мы отправились бродить по городу.

Вскоре мы вышли на широкую, светлую улицу, где стояли красивые дома из пластиката, стекла и алюминия. Разноцветные световые рекламы делали их особенно нарядными.

Улица называлась «Автоматическая». Мы подошли к большому зданию.

— «Выдача и прием призраков от трёх до четырёх часов», — прочитал Сева.

— Ну как ты читаешь?! — возмутилась Таня. — Не призраков, а признаков!

— Слава богу! А я уж испугался, — обрадовался Сева. — Признаки — это совсем другое дело.

— Ах, другое? — не унималась Таня, — Не объяснишь ли ты, что это за «другое»?

— Пожалуйста, — небрежно ответил Сева. — Вот, например, ехидство — признак дурного характера!

— А болтливость — признак глупости! — не осталась в долгу Таня.

— Чем попусту пререкаться, лучше зайдем и узнаем, о каких признаках речь, — сказал Олег.

Возразить против этого было нечего: он, как всегда, оказался прав.

Мы очутились в светлом зале. Сначала нам показалось, что там никого нет. Вдруг Сева дёрнул Таню за руку и указал глазами на маленькую Пятерку, стоявшую у стены.

Тихим, неуверенным голоском Пятёрка что-то говорила. Но кому? Ведь рядом совершенно никого не было!

И вдруг раздался голос невидимого собеседника. Это было как гром с ясного неба. Мы невольно посмотрели на стеклянный потолок.

Голос на миг умолк и сейчас же загремел снова, очевидно обращаясь к нам:

— Здравствуйте, люди! Мы вам рады! Меня зовут Автомат. Я обучаю эту достойную карликаншу делению целых чисел. Она собирается стать учительницей.

И тут мы увидели, что Пятерка стоит у огромной машины, занимающей целую стену. Посредине светился серебристый экран, окружённый разноцветными лампочками, которые то вспыхивали, то гасли. Внутри что-то постукивало, потрескивало. Иногда раздавался тоненький мелодичный звонок.

— Вы разрешите мне продолжить занятия? — любезно осведомился Автомат.

— Пожалуйста, — ответил Сева. — Мы тоже с удовольствием поучимся делению.

— Как, вы ещё не умеете делить? Хр-пр-тр! Извините, это моя самая маленькая шестерёнка повернулась не в ту сторону. Вы её расстроили.

— Нет, вы меня не поняли, вообще-то мы делить умеем.

— Ах, умеете? Ну, тогда совсем другое дело. Не хотите ли решить примерчик? Я как раз собирался предложить его моей юной ученице.

На экране засветились числа:

— Позвольте мне, — сказала Пятёрка. — Начнём по правилам: сначала делим тринадцать на девять…

— Хр-пр-тр! Чтобы ответить на мой вопрос, вовсе не нужно делить. Я собирался вас спросить: делится ли это число на девять? Да или нет?

— Как, вы хотите, чтобы мы сказали это сразу, не разделив числа? — изумился Сева.

— Вот именно!

— Но это совершенно невозможно! — воскликнула Таня.

— Отчего же? — с достоинством ответил Автомат. — Для этого стоит только взглянуть, какая лампочка загорелась над экраном. Посмотрите-ка.

— Красная! — крикнула Пятёрка.

— Ну вот, всё ясно. Раз загорелась красная, значит, это число на девять не делится. А теперь взгляните ещё раз на экран.

Там уже стояло совсем другое число:

— А теперь зажглась зелёная лампочка, — сообщила Пятёрка.

— Так и должно быть, потому что это число делится на девять.

— Это же очень просто, — сказала Пятёрка, — красная лампочка — число не делится на девять, зелёная — делится на девять.

— Ха-ха-ха! — засмеялся Автомат. — Это просто потому, что лампочки зажигаю я. А попробуйте-ка зажечь сами нужную лампочку. Ха-ха-ха!

Маленькая Пятёрка покраснела до ушей.

— Ну, не огорчайтесь, я пошутил, — утешил её Автомат. — Дело в том, что у чисел есть признаки, по которым можно с первого взгляда определить, желают ли они делиться на некоторые числа или не желают. К сожалению, я располагаю очень небольшим набором таких признаков. Поэтому, если кто-нибудь из вас найдёт новый, неизвестный нам признак делимости, немедленно сообщите мне. Это будет замечательно! Вы даже не можете себе представить, какую большую пользу принесёте людям. Мне известны признаки делимости чисел на 2, на 3, на 4, на 5, на 6… Даже на 10 и на 11. Ещё несколько признаков — и это всё!

— Расскажите о каком-нибудь признаке, — попросила Пятёрка. — Это очень интересно.

— В таком случае вернёмся к тем двум числам, которые я только что показывал на экране. Напомню их.

На экране появились числа: 135 227 и 264 852.

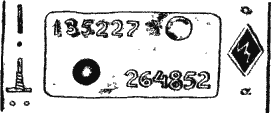Как видите, каждое число состоит из шести цифр. Будем эти цифры принимать за числа. И поставим между ними знаки плюс.

На экране под первым числом появилась сумма:

— А теперь скажите: делится ли число двадцать на девять? Нет, не делится. Значит, и все число тоже не делится на девять. Попробуем проделать то же самое со вторыми числом.

На экране снова засветилась сумма:

— Видите, получилось двадцать семь. А это число как раз делится на девять. Значит, и всё число тоже делится на девять. Вот каков признак делимости на девять. Его очень легко изложить так: число делится на девять, если сумма его цифр делится на девять.

— В таком случае, — сказал Олег, — я знаю и признак делимости на три. Ведь девять — это трижды три! Значит, если сумма цифр числа делится на три, то и само число тоже делится на три.

— Совершенно верно! Вы будете великим математиком! — торжественно изрёк Автомат.

— Я тоже знаю один признак: если сумма цифр числа делится на пять, то и число делится на пять, — сказал Сева. Ему тоже хотелось стать великим математиком.

— Ни в коем случае, ни в коем случае! — воскликнул Автомат, возмущённо замигав всеми своими лампочками. — Тр-пр-хр! Разве можно мерить всех одной меркой? Ведь число двадцать три не делится на пять, хотя сумма его цифр равна пяти. Признак делимости на пять очень прост: на пять делятся только те числа, которые оканчиваются пятёркой или нулём. Например, 75, 210, 625, 4 168 596 895 и так далее.

— Как просто! — засмеялась Таня.

— Есть признаки и посложнее. Например, признак делимости на одиннадцать.

— Ах, пожалуйста, расскажите об этом признаке! — попросила Пятёрка.

— Хорошо. Слушайте меня внимательно. Возьмём число

— У-у-у! — протянули ребята. — Это число и прочитать трудно.

— Хр-пр-тр! Сто семьдесят пять миллиардов триста шестьдесят два миллиона сто двадцать одна тысяча шестьсот девяносто три! — единым духом выпалил Автомат. — Ничего особенного. Посмотрим, делится ли оно на одиннадцать. Расположим цифры этого числа таким образом:

— Видите, я каждую вторую цифру опустил чуть пониже. А теперь поставим в каждом ряду между цифрами знаки плюс. Получаем:

В обоих рядах сумма цифр одинакова. А это и значит, что число непременно разделится на одиннадцать.

— Неужели? — усомнился Сева.

— Проверьте, — предложил Автомат.

— Это было бы слишком долго, — ответил Сева.

Тогда Олег показал нам страничку из блокнота, на которой он уже произвёл деление.

— Совершенно правильно! — сказал Автомат. — Вы действительно будете хорошим математиком.

А на экране вспыхнули числа:

— Вот вам и ответ: пятнадцать миллиардов девятьсот сорок два миллиона одиннадцать тысяч шестьдесят три.

— Значит, на одиннадцать делятся только такие числа, у которых сумма цифр, стоящих на нечётных местах, равна сумме цифр, стоящих на чётных? — спросил Олег.

— Нет, не только эти числа делятся на одиннадцать. Есть более общий признак делимости. Вот, например…

В это время раздался продолжительный звонок, возвестивший конец рабочего дня. Автомат едва успел с нами попрощаться, как все его лампочки погасли. Жаль!

Мы вышли на улицу. Теперь надо было поспеть на площадь Радостей и Огорчений, где нам назначила свидание Четвёрка с бантиком.

На этой площади ежедневно приземлялись воздушные корабли, возвращающиеся от людей в Карликанию.