ИДЕИ: Математика обмана: Можно ли победить мошенничество? и какой ценой?

Автор: Константин Богданов

Человек всесилен, и могущество его проистекает от общества, в котором он живет. На протяжении всей своей жизни мы используем и преумножаем достижения человеческого общества. Однако отношения между отдельным человеком и обществом остаются сложными.

Общество, открывая перед человеком широчайшие возможности, требует соблюдения определенных норм, тем самым ограничивая его свободу. На протяжении всей истории человечества общество учит своих граждан жить «по правилам». Некоторые из правил, которые общество навязывает гражданам, остаются неизменными с очень давних времен. Одно из них — «не обманывай!».

Честная конкуренция на рынке товаров и услуг — необходимое условие прогресса. Сговор участников рынка с целью обмана потребителей, как правило, приводит к необоснованному росту цен и зачастую препятствует развитию производства. Таким образом, излишнее стремление к личному обогащению отдельных граждан замедляет прогресс всего общества. Поэтому общество вынуждено защищаться от мошенников и наказывать их, тратя на это довольно много средств. Но когда процент мошенников становится выше определенного предела, то общество, будучи не в состоянии с помощью одних мошенников бороться с другими, значительно замедляет темпы развития (наказывая таким образом своих добропорядочных граждан). К сожалению, в каком-то смысле общество беззащитно перед мошенничеством, как перед эпидемией болезни, от которой не существует прививок.

Попробуем на очень простом примере проследить, как изменяется жизнь общества в зависимости от доли мошенников в нем. Пусть в городе имеется 100 таксомоторных парков, каждый из которых использует не более 100 машин. Кроме извоза, каждая из таксомоторных компаний (ТК) занимается ремонтом находящихся в эксплуатации автомашин, продавая их остальным компаниям, а взамен проданных покупает новые или бывшие в употреблении у других компаний. При этом некоторые ТК, пытаясь увеличить свою прибыль, сознательно завышают цены на продаваемые машины. Как зависит доход «честных» и «нечестных» ТК от процента честных ТК в городе?

Для упрощения моделирования будем считать, что каждая ТК раз в неделю сначала продает, а потом покупает один автомобиль у других ТК. Выбор продаваемого автомобиля случаен и определяется только его возрастом, который не должен быть меньше 3 лет (см. ниже, почему это так). ТК, покупающая выставленный на продажу автомобиль, выбирается компьютером случайно и должна обладать:

а) необходимым капиталом,

б) местом хотя бы для одной машины на стоянке и

в) желанием купить данную машину у данного продавца (см. случай мафиозного сговора ниже).

После того как ТК-покупатель найден, ТК-продавец, если он честный, продает машину за ее реальную цену, экспоненциально зависящую от возраста машины так, что она уменьшается в 20 раз за 10 лет. Если же ТК-продавец нечестен, то он искусственно завышает цену. Завышенная цена машины экспоненциально уменьшается с ее возрастом лишь в 2,72 раза за 10 лет (у честного продавца цена машины возраста t составляет e—0,3t, а у нечестного — e—0,1t от цены новой машины).

Легко показать, что наибольшие барыши, превышающие 1/3 стоимости новой машины, приносит мошенникам продажа автомобилей с возрастом от 3 до 9 лет. Поэтому торговать совсем новыми машинами им нет никакого смысла, да и при использовании в качестве такси новая машина даст больше выручки.

После того как машина продана, ТК-продавец, если ему позволяют средства, случайным образом ищет у остальных ТК подходящую машину взамен проданной, соблюдая правила (а)-(в), аналогичные тем, что действовали при продаже.

Инспекция таксомоторных компаний пытается контролировать сделки купли-продажи, штрафуя мошенников, когда их удается поймать с поличным. Работу инспекции характеризуют два параметра: вероятность q появления инспекторов в момент сделки и величина налагаемого ими штрафа F.

В конце каждой недели ТК подводят итоги своей коммерческой деятельности, учитывая доходы и расходы от продажи и покупки автомобилей, а также прибыль, поступившую от эксплуатации каждого автомобиля в качестве такси (она тоже экспоненциальным образом зависит от возраста автомобиля, уменьшаясь в 2,72 раза через 10 лет эксплуатации).

Если оказывается, что денежные средства компании падают ниже устанавливаемого предела (50% от начального капитала), то ее стратегия изменяется — ТК перестает покупать машины взамен проданных, пытаясь увеличить свой капитал. Нечестные ТК, у которых денежные средства упали ниже допустимого предела в результате штрафов за недобросовестную торговлю машинами, временно «становятся честными» и прекращают продавать машины по завышенным ценам.

Компьютерное моделирование взаимодействия сотен ТК по таким правилам на протяжении нескольких лет требует лишь нескольких минут машинного времени. В таблице 1 приведены параметры модели, которые были использованы в наших расчетах.

Чтобы никого не обижать, раздадим всем ТК одинаковый начальный капитал в 1 млн. долларов и по 98 машин. Сделаем так, чтобы «возрастной ассортимент» машин был одинаков у всех ТК, а возраст машин не превышал 9 лет.

Когда люди только начинают воровать, они стесняются и стараются никому не рассказывать о своем новом источнике доходов. Будем и мы сначала считать, что наши автомобильные мошенники — начинающие. Из этого следует, что таксомоторные компании, необоснованно увеличивающие цену машины при продаже, не знают остальных мошенников, и когда нечестные компании покупают друг у друга автомобили, то они из начинающих мошенников на время превращаются в жертвы. Однако, даже если не знать списка добросовестных компаний, продавать по завышенным ценам все-таки выгоднее, чем по честным — если, конечно, инспекторы в отпуске (см. рис. 1).

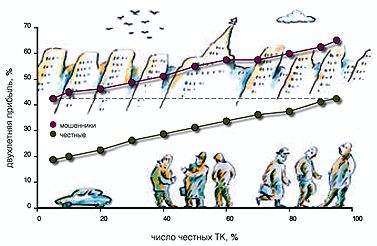Рисунок показывает результаты компьютерного моделирования в том случае, когда инспекция отсутствует, а недобросовестные компании ничего не знают друг о друге. Видно, что даже без инспекции честно работать прибыльно, и денежный капитал честных компаний увеличивается за два года на 20—40% . При этом их прибыль растет с увеличением доли честных компаний в городе. Такое же благоприятное воздействие оказывает рост доли честных ТК и на прибыль мошенников — чем больше честных ТК, тем больше прибыль у мошенников. Как иллюстрирует рис. 1, во всем диапазоне изменения доли честных ТК (от 0 до 100%) прибыль мошенников всегда больше. Однако обратите внимание на то, что прибыль у мошенников, когда в городе нет честных ТК (крайне левая точка на кривой с черными кружками), такая же, как у честных компаний, когда в городе нет мошенников ТК (крайне правая точка на кривой с белыми кружками). Таким образом, если воруют все, то нет никакого выигрыша по сравнению с тем случаем, когда все ТК в городе честные. Другими словами, мошенничество перестает приносить дополнительный доход, когда этим занимаются все.

Результаты моделирования, представленные на рис. 1, были получены в предположении, что инспекция отсутствует. Посмотрим, к чему может привести появление инспекторов. Сначала найдем необходимую частоту проверок, чтобы мошенничество перестало быть прибыльным. Для этого, очевидно, необходимо, чтобы мошенник платил штраф не меньший, чем доход (МД), полученный в результате мошенничества.

Если инспектор становится свидетелем преднамеренного завышения цены продаваемой машины, это превышение (МД) возвращается покупателю, а на продавца налагают штраф F. В результате суммарная величина штрафа оказывается равной F + МД. Пусть вероятность появления инспектора при совершении сделки — q, а мошенник ухитряется продавать в неделю по машине. Тогда средняя за неделю величина штрафа будет равна q·(F+МД). Приравнивая q·(F+МД) к МД, получаем минимальное значение для q, при котором мошенничество становится бесприбыльным (qmin),

qmin= МД / (F+МД). (1)

Для нашего случая (МД=$3670, F=$20000) qmin= 0,15. Посмотрим теперь на результаты компьютерного моделирования.

На рис. 2 изображены зависимости двухлетней прибыли честных и нечестных ТК от доли честных ТК в двух ситуациях — когда инспекции нет и когда она проводится с вероятностью 0,15. Как мы и ожидали, инспекция снижает прибыль нечестных ТК, приближая ее к прибыли честных. Однако линейная зависимость прибыли от доли честных ТК сохраняется. Кроме того, мошенники, несмотря на инспекторские рейды, продолжают обманывать и продавать машины по завышенным ценам, хотя в среднем уже не имеют от этого никакой выгоды. Иными словами, они предпочитают переждать инспекцию, сохраняя свои цены на автомобили.

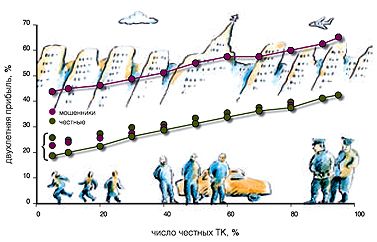Следует отметить, что такая частота инспекций не приносит никакой выгоды честным ТК, за исключением тех случаев, когда честных компаний очень мало (на рис. 2 фигурной скобкой показано увеличение их прибыли). Да это и не удивительно, так как инспекторы, наказывая мошенников, берут всю сумму F штрафа себе, а не перераспределяют ее среди честных ТК. Остаются в выигрыше от инспекции только те честные ТК, которые купили машину в присутствии инспектора, так как тогда им возвращают МД.

Таким образом, активность инспекторов, направленная на устрашение мошенников, становится полезной для честных ТК тогда, когда мошенников вынуждают продавать машины по честным ценам, делая из них добросовестных граждан. Если же инспекция приводит только к регулярным штрафам, то она становится бесполезной для города. Ну а если при минимальной частоте проверок qmin, вычисляемой по формуле (1), мошенничество остается-таки прибыльным, значит, либо мошенники знают о проверках, либо инспекторы тоже мошенники.

После того как мошенники, покупая друг у друга машины, оказываются обманутыми, им становится ясно, что лучше объединиться и продавать машины только честным ТК. Так, или почти так, появляется мафия — объединение мошенников, решивших воровать сообща. Посмотрим, как изменится ситуация в нашем компьютерном городе, когда все нечестные ТК договорятся не продавать машины друг другу, а честные ТК ничего не будут знать об этом сговоре.

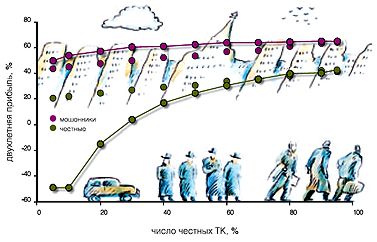Чтобы узнать, как мафия расправляется с честными ТК в отсутствие инспекторов, снова отправим последних в двухлетний отпуск и запустим программу. Рис. 3 показывает, как мафиозные отношения среди нечестных ТК изменяют их прибыль. Первое, что бросается в глаза, — отсутствие линейной зависимости прибыли от доли честных ТК в городе, как было в эпоху начинающих мошенников. При этом разница в прибыли нечестных и честных резко уменьшается с ростом доли честных в городе.

Отметим, что с увеличением числа честных ТК зависимости прибыли честных и нечестных ТК в условиях мафиозного сговора стремятся к соответствующим прямым, описывающим прибыли для эпохи начинающих мошенников. Да и максимальные значения прибыли у мафиози и начинающих одни и те же. И не удивительно, ведь эти значения просто пропорциональны произведению среднего барыша при торговле (МД) и числу недель (104), а также постоянной выручке от такси, которую даже мафиози не в силах изменить. Мафиозный сговор лишь делает более выгодными торговые сделки при малом числе честных ТК по сравнению со сделками начинающих мошенников. Однако, как и в эпоху начинающих мошенников, мошенничество теряет смысл, когда мошенники все.

Видно, что в условиях мафиозного сговора двухлетняя прибыль честных ТК при их относительно малом числе (5 и 10%) отрицательна (—50%) и соответствует тому значению денежного капитала, при котором ТК прекращают покупать машины, боясь разориться окончательно. Происходит это из-за мафиозного сговора между нечестными ТК, в результате чего среднее число обманов мафиози по отношению к честным ТК значительно возрастает по сравнению с эпохой начинающих мошенников.

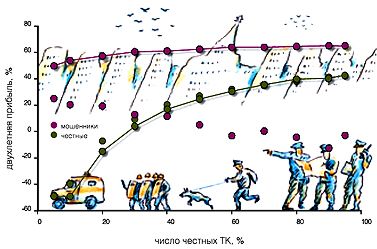
Рис. 4 показывает, как инспекция с частотой q=0,15 (15 случайных визитов на каждую ТК в течение 100 недель) и штрафом в $20000 меняет прибыль ТК. Оказывается, что параметры инспекции, бывшие эффективными при борьбе с начинающими мошенниками (см. рис. 2), перестают быть таковыми в случае мафиозного сговора. Только в тех случаях, когда число мошенников мало (lt; 20%), инспекции удается снизить их прибыль до уровня честных ТК. Ну а когда мошенников много, их прибыль остается гораздо выше, чем у честных ТК, даже при регулярных рейдах инспекции. Почему?

Происходит это из-за того, что мафиози исключили из своей практики незаконные операции между собой как не приносящие выгоды в среднем. И в результате вероятность быть схваченными на месте преступления у них снизилась по сравнению с эпохой начинающих мошенников. Поэтому и максимальные потери от инспекции мафиози несут в тех случаях, когда число честных велико, что совпадает с данными компьютерного моделирования (см. рис. 4). Ну а при малом проценте честных ТК штрафные санкции становятся неэффективным инструментом в борьбе с мафией.

Как было показано, обычная инспекция, выбирающая частоту проверок q по формуле (1), становится беспомощной, если нечестные ТК находятся в сговоре. Чтобы сделать штрафные санкции эффективными и при малом числе честных ТК, можно, очевидно, увеличить q или величину штрафа F еще в три-четыре раза. Рис. 5 показывает, как уменьшится прибыль мафиозных ТК при увеличении штрафа с $20000 до $70000. Как и ожидалось, такие высокие штрафы убирают мафиозную прибыль даже тогда, когда честных ТК очень мало, доводя ее до уровня эпохи честных ТК при начинающих мошенниках (см. рис. 1 для сравнения). У мафиозных ТК, окруженных большим числом честных, при высоких штрафах прибыль становится даже отрицательной, а работа — нестабильной, о чем говорит значительный разброс точек на соответствующей кривой.

Иногда в ответ на вопрос «Почему вы нарушаете закон?» мы слышим «Так ведь все так делают!» В случаях мошенничества интуитивно ясно, и мы это показали с помощью компьютерного моделирования, что если все вокруг занимаются мошенничеством, то они перестают извлекать из этого пользу. Даже само понятие воровства просто исчезает в этом сообществе, и его с экономической точки зрения можно считать обществом честных граждан, которые покупают друг у друга все товары и услуги по завышенным ценам. А прибыль каждого из граждан этого сообщества не изменится, если все «по команде» встанут на путь праведный.

Читатель, добравшийся до конца статьи, по-видимому, скажет, что в результате долгих рассуждений и компьютерного моделирования мы пришли, казалось бы, к двум тривиальным выводам: