"Искатели необычайных автографов" - читать интересную книгу автора

ВЕЗДЕСУЩАЯ МАТЕМАТИКА

Сгорбленный кривоглазый старик в полосатом тюрбане и засаленном халате долго вертел между скрюченными пальцами незнакомые монеты.

— Испанские? — спросил он наконец, сверля диковинных чужеземцев единственным, неестественно выпученным глазом.

Мате отрицательно покачал головой.

— Венецейские?

— Российские, — сказал Мате, уверенный, что меняла ни за что не захочет сознаться в своем невежестве.

Он не ошибся: поторговавшись для приличия (ибо какой уважающий себя финансист совершает сделки не торгуясь?), старый скупердяй отсыпал им горсть звонких монеток, и скоро друзья снова очутились подле жаровни с лепешками. Фило выбрал одну порумяней и поднес ко рту, но Мате остановил его.

— Неужели вы действительно собираетесь съесть эту лепешку? — спросил он с сожалением.

— А что же с ней еще делать? Носить на груди вместо медальона?

— Отчего бы и нет! У нее такая совершенная форма. Идеальное коническое сечение.

— Ну и пусть комическое, мне-то что! — нетерпеливо отмахнулся Фило и разом отхватил половину лепешки.

— Да не комическое, а ко-ни-чес-ко-е! Неужели вы никогда не читали знаменитого трактата о конических сечениях, написанного великим древнегреческим математиком Аполлонием Пергским?

Мате прекрасно понимал, что трактата Аполлония Фило и в глаза не видал, — просто ему хотелось пристыдить своего спутника. Но тот и не думал смущаться.

— Не угнетайте меня, пожалуйста, своей эрудицией, — заявил он независимо. — Еще Хайям учил: «Будь мягче к людям! Хочешь быть мудрей, — не делай больно мудростью своей!»

Мате очень хотелось ответить, что вовсе не он, а Фило угнетает его своей эрудицией. Но вместо того он молча вытащил из кармана потрепанный блокнот, вырвал из него листок бумаги, свернул кулечком и, аккуратно подогнув края, поставил к себе на ладонь.

— Как по-вашему, что это такое?

— Фунтик! — по-детски обрадовался Фило.

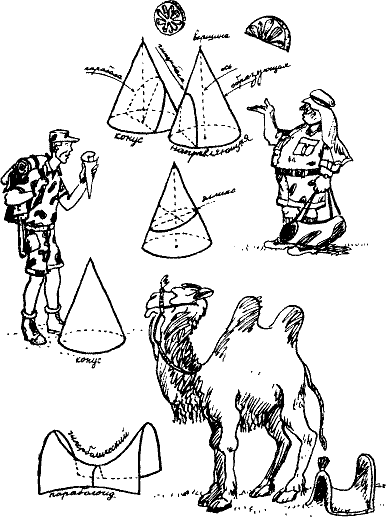
— Сами вы фунтик! — добродушно огрызнулся Мате. — Конус это. Круговой конус, то есть такой, у которого основание — круг. И, как у всякого порядочного кругового конуса, есть у него вершина и ось. Иначе говоря, перпендикуляр, опущенный из вершины на основание. Заметьте еще, что окружность основания называется направляющей, а прямая, которая соединяет вершину конуса с любой точкой этой окружности, — образующей конуса. Понимаете?

Фило неуверенно кивнул.

— Теперь возьмем плоскость, — не унимался Мате.

— Где возьмем?

— О Господи! В воображении, конечно. Итак, возьмем воображаемую плоскость и рассечем ею конус, ну, хотя бы параллельно оси. В этом случае на поверхности конуса появится линия, которая называется гиперболой. Видите?

Но нет, Фило ничего не видел.

— Полное отсутствие математического воображения, — констатировал Мате и карандашом нарисовал на поверхности фунтика кривую от воображаемого сечения.

— Вот вам гипербола. А теперь рассечем конус параллельно образующей. При этом на поверхности его получится линия, которая называется параболой. Вот она.

Фило отрывисто засмеялся.

— Интересно, как вы отличаете гиперболу от параболы? На мой взгляд, они совершенно одинаковы.

— Так то на ваш взгляд. А на самом деле…

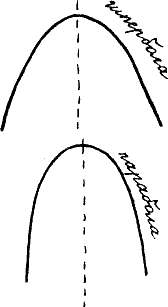
Мате снова достал блокнот и быстро начертил две кривые.

— Неужели вы и теперь не замечаете никакой разницы?

— Теперь замечаю, — снизошел Фило. — У гиперболы концы расходятся как у рогатки, а у параболы вроде бы держатся поближе, словно что-то их пригибает или притягивает друг к другу… Но при чем тут все-таки лепешки?

— Не беспокойтесь, дойдем и до лепешек, — заверил Мате. — На сей раз проведем такое сечение, которое не будет ни параллельным образующей, ни параллельным оси. В общем, нечто промежуточное между ними. И как вы думаете, что у нас при этом получится? У нас получится замкнутая кривая, которая называется эллипсом.

— Лепешка! — сейчас же установил Фило, взглянув на контур, нарисованный на фунтике. — Как сказано в «Евгении Онегине», увы, сомнений нет, я съел эллипс!

— Теперь никто не упрекнет вас в том, что вы не пробовали геометрии… Но шутки в сторону. На этом маленьком примере я хотел показать вам, что все на свете может быть выражено языком математики.

— Даже этот же четвероногий корабль пустыни? —

Фило указал на высокомерно жующего верблюда, мимо которого они проходили.

— Отчего бы и нет? Взгляните на поверхность, образованную его горбами. Великолепный образчик гиперболического параболоида.

Мате подошел к верблюду и провел ладонью по мохнатой седлообразной спине. Но верблюд, вероятно, был противником фамильярности: он отвернулся и сплюнул, да так выразительно, что друзья расхохотались.

— Видите, — торжествовал Фило, — плевал он на ваш параболический гиперболоид или как его там…

Тут раздались певучие выкрики:

— Дыни, дыни! Спелые дыни! Положи кусочек в рот — половина сахар, половина мед!

Продолговатые, обтянутые сетчатой кожей дыни произвели на Фило не меньшее впечатление, чем лепешки.

— Не хотите ли отведать ломтик этого восхитительного эллипса, Мате? — предложил он, желая щегольнуть вновь приобретенными познаниями.

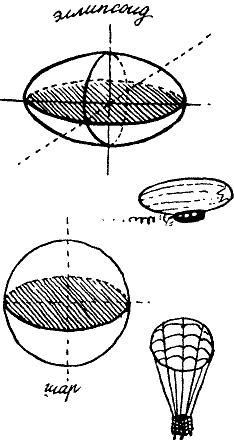
Но увы! Мате сказал, что дыня не эллипс, а эллипсоид вращения.

— Это что еще за фрукт?

— Скорее, продукт. Продукт вращения эллипса вокруг своей оси. При этом как раз и получается тело, напоминающее дыню.

— С вами не соскучишься! Не объясните ли заодно, что такое арбуз?

Фило надеялся, что Мате нипочем не ответит. Но тот преспокойно объявил, что арбуз — шар, иначе говоря, продукт вращения круга вокруг своего диаметра. А так как круг можно рассматривать как частный случай эллипса, то есть как эллипс, у которого все оси одинаковы, стало быть, шар есть частный случай эллипсоида.

Фило опешил. Что ж это делается?! Выходит, арбуз — частный случай дыни? Но Мате не нашел в его выводе ничего нелепого. Наоборот! По его мнению, Фило начинает рассуждать как настоящий математик. Тот хмуро поклонился.

— Приятно слышать. Но, откровенно говоря, до сих пор я себе нравился больше. Как сказано в «Евгении Онегине», «куда, куда вы удалились, весны моей златые дни». Где то прекрасное время, когда я ел арбуз, не подозревая, что он — частный случай дыни? Где, скажите мне, та счастливая пора, когда я воспринимал мир непосредственно, не размышляя, не думая о том, что он такое с точки зрения математики?

— Вас послушать, так размышление свойственно только науке, — колко возразил Мате. — А разве ваше дражайшее искусство не рассуждает, не анализирует, не пытается осмыслить действительность?

— Да, пытается. И осмысливает. Но своими средствами. Без помощи гиперболического параболоида. — Фило постучал пальцем по груди. — С помощью сердца. А сердце, милостивый государь, математике не подвластно. Сердца математикой не проанализируешь.

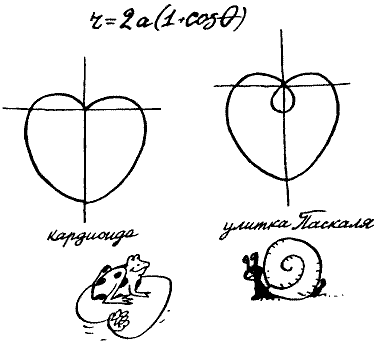
— Ошибаетесь, — холодно сказал Мате. — Сердце — это не что иное, как «эр», равное двум «а», умноженным на единицу плюс косинус тэта.

— Мате, голубчик, что вы такое говорите! — не на шутку встревожился Фило. — Вы не заболели?

Но Мате не заболел. Просто, сказал он, есть в математике такая кривая, очень похожая на сердце, каким его обычно рисуют влюбленные, только без стрелы. Называется она кардиоидой. От греческого слова — «кардиа» — «сердце». Ее-то уравнение он и привел.

Мате снова вытащил свой видавший виды блокнот, нарисовал кардиоиду и показал Фило.

— В самом деле, похоже, — криво усмехнулся тот. — И кто это только выдумал?

— Один ученый, о котором вы, конечно, не знаете. Паскаль.

— За кого вы меня принимаете! — оскорбился Фило. — Могу ли я не знать о человеке, из-за которого получал в детстве двойки? У него еще есть закон о давлении чего-то там на что-то…

— Во-первых, не чего-то на что-то, а жидкости и газа на стенки сосуда. А во-вторых, мы с вами говорим о разных Паскалях. Вы имеете в виду великого французского ученого семнадцатого века Блеза Паскаля, а я — его отца, Этьена Паскаля, тоже замечательного математика. Именно он изучал кривую, которая получила название улитки Паскаля. — Мате нарисовал замкнутую самопересекающуюся кривую с петелькой внутри. — Видите, эта петелька может увеличиваться и уменьшаться. Когда она исчезает совсем, улитка Паскаля превращается в кардиоиду.

Фило сосредоточенно ощупал левую сторону груди. Как же так? Неужели, с точки зрения математики, сердце — всего-навсего частный случай какой-то улитки?!

Острые глазки Мате потеплели, засветились добродушной хитрецой. Мог ли он предполагать, что Фило не понимает научного юмора? Ведь кардиоида — не сердце, а всего лишь сходная с ним кривая. А говоря о кривых, не стоит быть слишком прямолинейным.

— Ага! — закричал Фило. — Значит, вы признаете, что человеческое сердце и математический расчет — две вещи несовместные?

— Ну, это еще неизвестно. Строение живых организмов — предмет пристального внимания инженеров, которые ищут в природе прообразы своих будущих сооружений. Природа, знаете ли, на редкость изобретательный конструктор. У нее есть чему поучиться. Возьмите, к примеру, летучую мышь…

— Ни за что! — Фило брезгливо поморщился. — Я их терпеть не могу.

Мате пожал плечами: за что такая немилость? Летучие мыши не только совершенно безобидны, но даже полезны. Они уничтожают вредных насекомых, и как раз в такое время, когда делать это абсолютно некому, — ночью.

— Вслепую?! — изумился Фило.

— В том-то и дело!

И Мате принялся рассказывать.

Оказывается, зрение у летучей мыши очень слабое. Но природа снабдила ее таким свойством, которое с лихвой восполняет этот недостаток. При полете она непрерывно издает неслышные для нас ультразвуки. Отражаясь от встречных предметов, звуковые волны возвращаются к ней обратно и предупреждают о приближении препятствия. Вот почему летучая мышь стала прообразом радиолокатора.

А птицы? Они с незапамятных времен служили людям моделью летательных аппаратов. Впрочем, чтобы летать по-настоящему, человеку недостаточно скопировать птичьи крылья. На поверхностном, нетворческом подражательстве далеко не улетишь.

Первым понял это гениальный русский ученый Жуковский. Помимо строения птиц, он изучил особенности их полета, взаимосвязь между формой крыла и сопротивлением воздуха. Исследование Жуковского «О парении птиц» стало тем зерном, из которого выросло современное самолетостроение. Благодаря ему поднялись в воздух тяжелые, мощные машины, за которыми не угнаться не то что птице, но даже звуку…

— Да, много загадок задает нам природа, — задумчиво продолжал Мате. — Кораблестроители, например, очень сейчас заинтригованы причинами необычайной быстроходности дельфинов. Одна из этих причин уже установлена. Это особое строение кожи. Ученым удалось создать резиновое подобие дельфиньей кожи, которой обтянули подводные лодки. И знаете, быстроходность лодок значительно возросла… А пауки? Разве не интересно докопаться, что дает им возможность выпускать нить такой невероятной прочности? Конечно, на первый взгляд — паутина и прочность — понятия несовместимые. Но испытайте на разрыв нить паутины и той же толщины стальную проволоку — и вы убедитесь, что паутина много прочнее. В Южной Америке водятся пауки, паутина которых вполне заменяет рыбачьи сети. Что, не верите? Думаете, я преувеличиваю?

— Думаю, но совсем не то, — сказал Фило, глядя на друга восторженными глазами. — Думаю, что вы поэт.

Вот чего Мате не ожидал. Он — поэт? Что за глупая выдумка! Но Фило настаивал на своем: Мате настоящий поэт науки.

— Знаете, — признался он, — когда вы говорили, я вдруг почувствовал гордость. Да, гордость. За человека, за его разум, за его безграничные возможности…

— Будет вам, — отмахнулся Мате, очень, впрочем, довольный. — Лучше скажите, какого мнения об этом ваш Хайям. Есть у него что-нибудь о человеке и его возможностях?

— У Хайяма все есть! Вот, слушайте:

Состязаться с Хайямом было трудно. Друзья задумались и шли некоторое время молча.

— Нет, — неожиданно заявил Мате, — так больше продолжаться не может. С этой минуты мы начинаем искать Хайямов по-настоящему.

И он быстро зашагал вперед, решительно раздвигая толпу и громко выкрикивая на ходу.

— Хайям! Хайя-а-ам! Хайя-а-а-а-ам!

— Это от жары! — трагически прошептал Фило и бросился за ним.