"Путевые заметки рассеянного магистра" - читать интересную книгу автора (Левшин Владимир Артурович)
ТРИНАДЦАТОЕ ЗАСЕДАНИЕ КРМ
намечено было провести в школьном спортзале, но преподаватель физкультуры, узнав, что шестой член нашего клуба — существо собачьей породы, запротестовал. Пришлось взять грех на душу и пообещать ему, что Пончик будет вести себя смирно и вежливо, хоть особой уверенности в этом ни у кого из нас не было. Словно в благодарность за поручительство, Пончик и впрямь был тих, как мышка. Всем на удивление, он залаял всего один раз, и то, когда смолчать было бы невмоготу и немому.
Встреча наша началась с небольшой разминки. Ребята поиграли в баскетбол: Сева и Нулик против Тани и Олега. Матч, который судили мы с Пончиком, окончился вничью, после чего первым обсуждение начал президент: ему опять не терпелось высказаться по географическим вопросам…
— Озеро Чад очень мелководно, — зачастил он без знаков препинания, — глубина его в среднем около полутора метров,
поэтому нечего было Магистру ожидать мощного теплохода плоскодонка самое милое дело для такого озера а шест ему дали не затем чтобы грести а чтобы отталкиваться от дна и никаких навигационных приборов на плоскодонке не бывает а насчёт символа дружбы передаю слово другому оратору потому что ничего об этом не знаю… Уф!
Нулик брякнулся на скамью и долго ещё «отдышивался», прислушиваясь к выступлению Тани.
— Напомню, — сказала она, — что дно плоскодонки имело форму правильного пятиугольника, и Единичка верно поступила, вычертив на нём диагонали. Ведь у неё получилась пятиконечная звезда! А это и есть пифагоров символ дружбы.
— Выходит, пятиконечная звезда считалась символом дружбы и в древности, а не только в наше время! — удивился Сева.
— Выходит. Звезда у пифагорейцев была чем-то вроде талисмана, которым одаривали друзей. Однажды некий пифагореец, скитаясь где-то далеко от родины, заболел. Какой-то добрый человек приютил его в своём доме и ухаживал за ним до самой его кончины. Перед смертью больной посоветовал хозяину нарисовать на своём жилище пятиконечную звезду. Несколько лет спустя попал в эту страну другой пифагореец. Увидав дом с пятиконечной звездой на стене, он тотчас понял, что здесь побывал его собрат-пифагореец, и щедро отблагодарил заботливого хозяина.
— Но почему Пифагор выбрал именно этот символ? — спросил Нулик.
— А потому, что считал эту фигуру удивительной. Она и впрямь удивительна. Неспроста Единичка, вычерчивая её, всё время приговаривала: «Ай да золото!»
— Может быть, у плоскодонки было золотое дно? — предположил Нулик.
— Да нет, дно было баобабовым, а вот свойства пятиконечной звезды и в самом деле чистое золото. Это и подметил Пифагор.
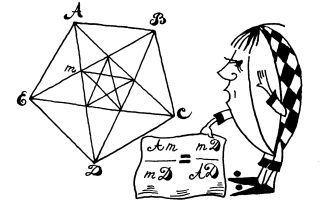
Таня разложила на полу большой чертёж с изображением правильного пятиугольника. Внутри пятиугольника она провела пять диагоналей, которые образовали пятиконечную звезду с вершинами в точках A, B, C, D и E.
Склонившись над чертежом, ребята пристально вглядывались в фигуру.
 |
— Ой, — закричал Нулик, — что я заметил! Внутри звезды ещё пятиугольник, а в нём ещё звезда. И так без конца…
— А если б ты был ещё внимательней, — сказала Таня, — то заметил бы, что диагонали большого пятиугольника делят угол при его вершинах на три угла, каждый из которых равен 36 градусам.
— Выходит, угол при вершине пятиугольника равен 108 градусам, — подсчитал Нулик.
— А сумма пяти углов звезды — 180, — сообразил Сева. — Совсем как у треугольника. Действительно замечательная фигура!
— Это что! — возразила Таня. — Самое замечательное свойство звезды впереди. Рассмотрим какую-нибудь из её сторон, то есть диагональ пятиугольника, — вот хотя бы диагональ AD. Диагональ эту в точке
Нулик вопросительно вскинул брови: — Ну и что?
— А то, что меньший отрезок A
A
— Но отсюда вытекает, что
— Очень хорошо, — одобрила Таня. — Это и называется разделить сторону AD в среднем и крайнем отношениях. Сева хлопнул себя по лбу:
— Так вот о чём говорила Единичка! Только при чём здесь всё-таки золото?
— А при том, что такое деление Пифагор и его последователи называли золотым делением или золотым сечением.
— Такую пропорцию называли ещё божественной, — добавил Олег.
— Как раз об этом я и хотела сказать. Древние широко использовали божественную пропорцию в искусстве. Они проверяли ею красоту человеческого тела и признавали его идеальным лишь тогда, когда соотношения отдельных его частей подчинялись закону золотого сечения.
Таня извлекла из портфеля фотографию, испещрённую горизонтальными линиями.
— Вот статуя Аполлона Бельведерского, который, как известно, считается идеалом человеческой красоты. Все пропорции этой фигуры, все её соотношения, строго соответствуют золотому сечению: верхняя и нижняя части торса, ноги, руки…
— Чего нельзя сказать о Магистре, — сокрушённо вздохнул Сева. — Единичке очень не понравились его пропорции. Видно, далеко ему до Аполлона…
— Да и тебе не близко, — сказала Таня, критически оглядев Севу.
— Золотому сечению соответствовали и пропорции греческих зданий, — торопливо сказал Олег, чтобы прекратить неприятную пикировку. — Оттого они и до сих пор остаются для нас образцом красоты и гармонии.
— И все это придумал Пифагор, — заключил Нулик. — Силён!
— Пифагор, конечно, силён, — подтвердил я, — но справедливости ради надо сказать, что золотое сечение было известно ещё в Древнем Вавилоне. Да и вообще правило это выдумано не человеком, а самой природой. Пифагор только подметил его. И здесь время вспомнить о засушенной веточке, которую так расхваливала Единичка.
— У-у-у, — протянул Нулик, — а я думал, она это просто так…
— Пора бы уже заметить, что Единичка ничего не говорит просто так. Посмотрите-ка на эту веточку. Нет, это не Единичкина, а моя. Но взгляните, как расположены на ней листья. Попробуйте измерить расстояния между ними.
Сева порылся в кармане (а там чего-чего только нет!), извлёк сантиметр и принялся за измерение.
— Между первым листом и третьим, считая снизу, — 20 миллиметров, между первым и вторым — 12,5.
— Неточно, — сказал Нулик, ревниво следивший за операцией. — 12,36 миллиметра, а не 12,5.
 |
Я похвалил Нулика за педантичность и предложил установить, в какой пропорции второй лист делит расстояние между первым и третьим.
— Минуточку! — Сева вынул карандаш и блокнот. — 20 минус 12,36 — это 7,64. Таково расстояние между вторым и третьим листьями. Значит, 7,64 так относится к 12,36, как 12,36 относится к 20.
7,64:12,36 = 12,36:20.
— Но это и есть золотая пропорция! — подытожил я. — Ведь отношение верхнего деления к нижнему равно здесь отношению нижнего деления к общему расстоянию между крайними листьями. Как видите, природа — отличный художник. У неё верный глазомер и тонкое чувство гармонии.
— Ну, это ещё надо проверить! — изрёк Нулик (этого хлебом не корми — дай ему попроверять!).
— Проверяй, кто ж тебе мешает.
— Легко сказать, а как?
— Эх ты, Фома неверующий! Перемножь крайние и средние члены пропорции и увидишь, что оба произведения одинаковы.
— Действительно, — степенно процедил Нулик, поколдовав над клочком бумаги. — 7,64, умноженное на 20, равно 152,8. И 12,36, умноженные на 12,36, — это тоже 152,8. Природа, оказывается, не глупее Пифагора…
При этих словах все невольно обернулись к окну да так и ахнули:
— Снег! Первый снег!..
Вот тут и залаял Пончик. Он сразу понял, что произошло нечто удивительно радостное, и через мгновение вместе с другими членами клуба был уже во дворе.
Видимо, снег ему понравился: попробовав его на вкус, он удовлетворённо фыркнул и принялся энергично разгребать передними лапами.
— Смотрите-ка, — хохотал Нулик, — Пончик занялся археологическими раскопками.
Олег воспользовался этим обстоятельством по-своему:
— Умный пёс! Это он намекает, что пора спуститься вслед за Магистром в пещеру, где собраны разные окаменелости.
Президент втянул голову в плечи.
— В таком случае, берегите лбы, а то расшибётесь об эти… как их там… столо… стило…
— Только не называй их, как Магистр, сталагми#769;тами. Вернее всего, в пещере были сталакти#769;ты — ведь они свисали с высокого свода, как сосульки с крыши. А сталагмиты, наоборот, поднимаются снизу вверх.
— Сталактиты, сталагмиты… Не все ли равно, обо что расшибаться. Шишка так и так вскочит! — философски заметил Нулик. — Лучше скажи, чей всё-таки череп попался Магистру: андерт
Таня всплеснула руками:
— Ну и невежда! Пора бы уж знать, что неандерталец — не два, а одно слово. И появилось оно в прошлом веке, когда в Германии, в Неа#769;ндертале — в долине реки Неа#769;ндер, — был найден череп первочеловека. Что же касается андертальцев, то они существуют только в воображении Магистра…
— И ещё не мешает тебе знать, — продолжил Сева, — что учёные считают неандертальца, то есть первочеловека, переходным звеном между питека#769;нтропом (иначе говоря, обезьяночеловеком) и человеком нынешним, так сказать, нашего образца…
— Ага! — воодушевился Нулик, но тут же задумался. — А ведь Магистр утверждал, что эти самые люди нашего образца жили уже миллионы лет назад, в самом конце четвёртого периода…
— Не четвёртого, а четвертичного, — поправил его Олег.
— Все одно! — отмахнулся Нулик. — И ещё Магистр заявил, что относится этот четвертичный период к самой что ни на есть древней эре… как её… кай… най…
— Ты хочешь сказать — кайнозойской? — засмеялся Олег. — Но тут Магистр все перепутал. Самая древняя эра называется азойской (или архейской). А кайнозойская — это наша, новая эра. И название её произошло от двух греческих слов: «кайнос» — новый и «зое» — жизнь.
— А что это за азойская эра? — спросил Нулик.
— Эра, когда ещё никакой жизни и в помине не было. Ведь буква «а» в начале слова означает отрицание, — разъяснил Олег.
— Выходит, Магистр малость промахнулся?
— Ну да. Сказал, что встреченные им люди жили давным-давно, в самом конце четвертичного периода. Но ведь четвертичный период ещё продолжается и конца ему пока что не предвидится.
— Значит, Магистр увидел наших современников? — развёл руками Нулик.
— Вот именно, — подтвердила Таня. — А принял их за неандертальцев и питекантропов.
Нулик схватился за голову:
— Неандертальцы! Питекантропы! Да ну вас совсем. На дворе снег, а они… Объявляю перерыв! Президент я или не президент?!
— Президент, президент! — успокоил его Олег. — Но остались-то нам сущие пустяки — всего два вопроса…
— К тому же первый из них — игра, — поддержал Сева. — Вот и сыграем. Для наглядности.
У президента заблестели глаза.
— Прямо тут, во дворе?
— Во дворе, на снегу, — улещала Таня.
Предложение было слишком заманчивым, и Нулик, еле сдерживаясь, чтобы не завизжать от удовольствия, принялся вместе со всеми вычерчивать на снегу Луну и Солнце, вбивать столбики — словом, готовить всё необходимое.
Когда работа была закончена, Сева вынул из кармана пачку заготовленных дома бумажек с номерами. Каждый вытащил билетик наугад, а один оставшийся — номер 5 — достался Пончику. Вот она, собачья жизнь: не можешь вытащить номер сам, бери тот, что не вытащили другие!
Сева обвёл глазами заснеженное пространство, на котором резко чернели две правильные окружности.
— Начнём?
— Начнём! — сказал президент и одним прыжком очутился на Луне, но тут же снова спустился с небес на землю. — А для чего, собственно, нам играть?
— Что за вопрос? — удивилась Таня. — Чтобы выяснить ошибки Магистра.
— Но ведь на сей раз Магистр ни в чём не ошибся.
Олег посмотрел на Нулика поверх очков.
— Ты думаешь? Тогда сыграем для собственного удовольствия.
Тут уж президент не заставил себя упрашивать. Отчего бы и не побегать с одного круга на другой, особенно когда знаешь, что набегаешься досыта: как-никак впереди целых 720 перестановок! Но каково же было разочарование Нулика, когда после пятой перестановки игроки, в третий раз переселившись на Солнце, стояли уже в первоначальном порядке: 1, 2, 3, 4, 5 и 6. А это означало, что игре конец.
— Как же так? — недоумевал президент. — Ведь из шести чисел получается 720 перестановок!
— Что правда, то правда, да игра-то к перестановкам никакого отношения не имеет.
— Так, значит. Магистр ошибся?
— А ты — вслед за ним.
Сева со смехом толкнул Нулика в снег — и пошла кутерьма!
— Ой, щекотно!.. Ой, не могу!.. — отбивался президент.
— А ошибаться можешь?
— Один раз не в счёт!
— Один? Как бы не так!
— Да ну?!
Нулик даже привстал от неожиданности. Он был очень забавен в эту минуту: раскрасневшийся, взъерошенный, весь в снегу.
— Вот те и ну! Ты не заметил, что Магистр ошибся дважды: сперва, когда сказал про перестановки, а потом — когда написал, что все шесть игроков при каждом переходе с одного круга на другой занимали другое по счёту место от столба.
— А разве не так?
— Хочешь убедиться? Сыграем ещё разок.
— А ведь действительно! — сказал президент задумчиво, после того как был сыгран второй тур. — Менялись местами все, кроме Пончика.
— Значит, кроме номера 5, — уточнил Сева. — Он всегда оставался на пятом делении от столба.
— Выходит, передвигались с места на место всего пять, а не шесть игроков?
— В том-то и дело!
И тут Нулика осенило:
— Так вот почему Единичка хотело назвать эту игру «Упрямая пятёрка»!
Таня молитвенно воздела сложенные ладони.
— Слава тебе господи! Наконец-то дошло…
— Не такой уж я недогадливый, — обиделся президент.
Сева хитро прищурился:
— Это ещё надо проверить!
Излюбленное изречение Нулика, обращённое против него самого, возымело сильнейшее действие. Задетый за живое, президент раззадорился и разделал задачу с орехами, что называется, под орех. Он неопровержимо доказал, что если чан наполнен орехами на одну четверть и каждые пятнадцать минут туда ссыпают столько же орехов, сколько в нём уже есть, то спустя пятнадцать минут чан наполнится наполовину, а ещё через четверть часа он будет полон. Вот хитрюга Единичка и попросила Магистра подождать всего каких-нибудь полчасика!
— По-моему, — сказал я, — последнее попадание президента с лихвой искупает его предыдущие промахи. И так как чан наполнен, а ошибки Магистра исчерпаны, заседание можно бы и закрыть…
Все охотно со мной согласились, тем более что давно было пора обедать.
| © 2024 Библиотека RealLib.org (support [a t] reallib.org) |