"Статистика: учебное пособие" - читать интересную книгу автора
1.2. Методы измерения обобщающих характеристик совокупности
Метод группировок позволяет изучить состояние и взаимосвязи экономических явлений, если группы будут охарактеризованы показателями, раскрывающими наиболее существенные стороны изучаемого явления.
При анализе и планировании необходимо опираться не на случайные факты, а на показатели, выражающие основное, типичное, коренное. Такую характеристику дают различные виды средних величин, а также мода и медиана.
Вопрос об однородности совокупности не должен решаться формально по форме ее распределения. Его, как и вопрос о типичной средней, нужно решать, исходя из причин и условий, формирующих совокупность. Однородной является такая совокупность, единицы которой формируются под воздействием общих главных причин и условий, определяющих общий уровень данного признака, характерный для всей совокупности.
Согласно теории типологических группировок, решающее значение в оценке однородности совокупности принадлежит не форме распределения, а размеру вариации и условиям ее формирования. Для качественно однородной совокупности характерна вариация в определенных пределах, после чего начинается новое качество. Вместе с тем к этим границам для оценки качественной однородности совокупности надо подходить с точки зрения существа дела, а не формально, так как одно и то же количество в разных условиях выражает новое качество. Например, при одной и той же численности рабочих предприятия одних отраслей промышленности являются крупными, а других – мелкими.
Для всестороннего и углубленного изучения явлений, для объективной характеристики типов явлений, их взаимоотношений и процессов, обусловленных развитием системы как целого, необходимо сочетать групповые средние с общими средними. Сочетание таких средних и является одним из основных элементов анализа сложных систем. Это сочетание связывает в одно целое два органически дополняющих друг друга статистических метода: метод средних величин и метод группировки. При расчете средней индивидуальные варьирующие по группе значения заменяются одним средним значением. При этом случайные отклонения значения признака по отдельным единицам в сторону увеличения или уменьшения взаимно уравновешиваются и погашают друг друга, а в величине средней проявляется типичный размер признака, свойственный данной группе. Средняя величина служит характеристикой совокупности и в то же время относится к отдельному ее элементу – носителю качественных особенностей явления. Значение средней вполне конкретно, но одновременно и абстрактно; оно получено путем абстрагирования от случайного индивидуального по каждой единице с целью выявления того общего, типичного, что свойственно всем единицам и что формирует данную совокупность. При расчете средней величины численность единиц совокупности должна быть достаточно большой. Величина средней определяется как отношение общего объема явлений к числу единиц совокупности в группе. Для несгруппированных данных это будет средняя арифметическая простая:
 |
а для сгруппированных данных, где каждое значение признака имеет свою частоту, – средняя арифметическая взвешенная:
 |
где
Поскольку средняя арифметическая рассчитывается как отношение суммы значений признака к общей численности, она никогда не выходит за пределы этих значений. Средняя арифметическая обладает рядом свойств, которые широко используются в целях упорядочения расчетов.
1. Сумма отклонений индивидуальных значений признака от средней величины всегда равна нулю:
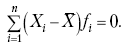 |
Разделив левую и правую часть на
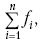 |
получим:
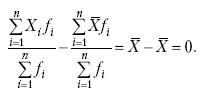 |
2. Если значения признака (Xi) изменить в
Среднюю арифметическую из новых значений признака обозначим X, тогда:
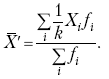 |
Постоянную величину 1/
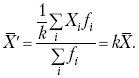 |
3. Если из всех значений признака
Средняя из отклонений значений признака от постоянного числа будет равна:
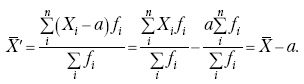 |
Точно так же доказывается это и в случае прибавления постоянного числа.
4. Если частоты всех значений признака уменьшить или увеличить в
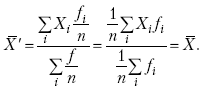 |
При наличии данных об общем объеме и известных значениях признака, но неизвестных частотах для определения среднего показателя используют формулу среднеарифметической взвешенной.
Например, имеются данные о ценах реализации капусты и общей выручке за различные сроки реализации (табл. 1).
Цена реализации капусты и общая выручка за различные сроки реализации
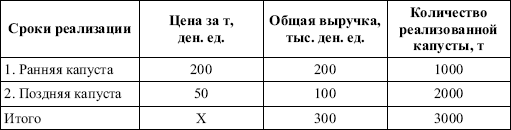 |
Так как средняя цена представляет отношение общей выручки к общему объему реализованной капусты, то вначале следует определить количество реализованной капусты по разным срокам реализации как отношение выручки к цене, а затем уже определить среднюю цену реализованной капусты.
В нашем примере средняя цена будет:
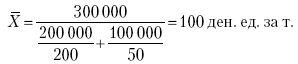 |
Если рассчитать в данном случае среднюю цену реализации по средней арифметической простой, то получим иной результат, который исказит истинное положение и завысит среднюю цену реализации, так как не будет учтен тот факт, что большая доля в реализации приходится на позднюю капусту с более низкой ценой.
Иногда требуется определить среднюю величину, когда значения признака даются в виде дробных чисел, т. е. обратных целым числам (например, при изучении производительности труда через обратный его показатель, трудоемкость). В таких случаях целесообразно использовать формулу средней гармонической:
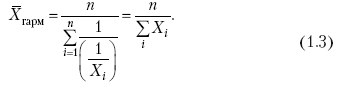 |
Так, среднее время, необходимое для изготовления единицы продукции, есть средняя гармоническая. Если Х1 = 1/4 часа, Х2 = 1/2 часа, Х3 = 1/3 часа, то средняя гармоническая этих чисел есть:
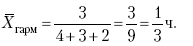 |
Для расчета средней величины из отношений двух одноименных показателей, например темпов роста, применяется средняя геометрическая, рассчитанная по формуле:
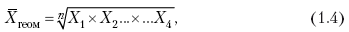 |
где Х1× Х2 … × … Х4 – отношение двух одноименных величин, например цепных темпов роста;
Рассмотренные средние величины обладают свойством маорантности:
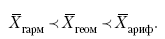 |
Пусть, например, имеем следующие значения
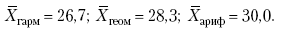 |
При изучении состава совокупности о типичном размере признака можно судить по так называемым структурным средним – моде и медиане.
Модой
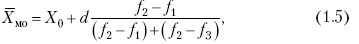 |
где Х0 – нижняя граница модального интервала;
Значение моды в интервальном ряду довольно просто можно отыскать на основе графика. Для этого в самом высоком столбце гистограммы от границ двух смежных столбцов проводят две линии. Из точки пересечения этих линий опускают перпендикуляр на ось абсцисс. Значение признака на оси абсцисс и будет модой (рис. 2).
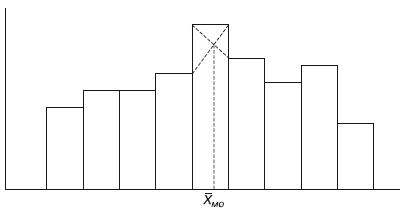 |
Рис. 2
Для решения практических задач наибольший интерес представляет обычно мода, выраженная в виде интервала, а не дискретным числом. Объясняется это назначением моды, которая должна выявить наиболее распространенные размеры явления.
Средняя – величина, типичная для всех единиц однородной совокупности. Мода – тоже типичная величина, но она определяет непосредственно размер признака, свойственный хотя и значительной части, но все же не всей совокупности. Она имеет большое значение для решения некоторых задач, например для прогнозирования того, какие размеры обуви, одежды должны быть предназначены для массового производства, и т. д.
Медиана
Медиана является лучшей характеристикой центральной тенденции, когда границы крайних интервалов открыты. Медиана является более приемлемой характеристикой уровня распределения и в том случае, если в ряду распределения имеются чрезмерно большие или чрезмерно малые значения, которые оказывают сильное влияние на среднюю величину, а на медиану – нет. Медиана, кроме того, обладает свойством линейного минимума: сумма абсолютных значений отклонений величины признака у всех единиц совокупности от медианы минимальная, т. е.
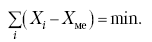 |
Это свойство имеет большое значение для решения некоторых практических задач – например, для расчета самого короткого из всех возможных расстояний для разных видов транспорта, для размещения станций техобслуживания таким образом, чтобы расстояние до всех обслуживаемых данной станцией машин было минимальным, и т. п.
При отыскании медианы сначала определяется ее порядковый номер в ряду распределения:
 |
Далее, соответственно порядковому номеру, по накопленным частотам ряда находят саму медиану. В дискретном ряду – без всякого расчета, а в интервальном ряду, зная порядковый номер медианы, по накопленным частотам отыскивается медианный интервал, в котором путем простейшего приема интерполяции определяется уже значение медианы. Расчет медианы осуществляется по формуле:
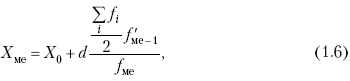 |
где
Рассчитаем среднюю величину, моду и медиану на примере интервального распределения. Данные приведены в табл. 2.
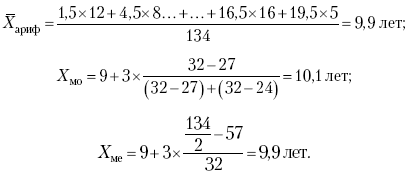 |
Таким образом, в качестве центра распределения могут быть использованы различные показатели: средняя величина, мода и медиана,
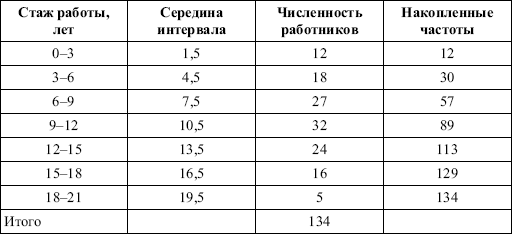 |
и каждая из этих характеристик имеет свои особенности. Так, для средней величины характерно то, что все отклонения от нее отдельных значений признака взаимно погашаются, т. е.
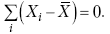 |
Для медианы характерно то, что сумма отклонений индивидуальных значений признака от нее (без учета знаков) является минимальной. Мода же характеризует наиболее часто встречающееся значение признака. Поэтому в зависимости от того, какая из особенностей интересует исследователя, и должна выбираться одна из рассмотренных характеристик. В отдельных случаях рассчитываются все характеристики.
Их сравнение и выявление соотношений между ними помогает выяснить особенности распределения того или иного вариационного ряда. Так, в симметричных рядах, как в нашем случае, все три характеристики (средняя, мода и медиана) примерно совпадают. Чем больше расхождение между модой и средней величиной, тем более асимметричен ряд. Установлено, что для умеренно асимметричных рядов разность между модой и средней арифметической примерно в три раза превышает разность между медианой и средней арифметической:
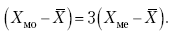 |
Это соотношение можно использовать для определения одного показателя по двум известным. Из этого следует, что сочетание моды, медианы и средней важно и для характеристики типа распределения.
| © 2024 Библиотека RealLib.org (support [a t] reallib.org) |