"Криптография и свобода" - читать интересную книгу автора (Масленников Михаил)
Freedom not free!
Глава 4. Шифры на новой элементной базе
Про шифры на новой элементной базе я уже несколько раз упоминал в этой книге, но в основном абстрактно: были заложены основы, велись теоретические разработки. А как пощупать их руками? Что в них было действительно нового?
Здесь надо немного окунуться в ту «докомпьютерную» эпоху. Что такое микропроцессор – представление об этом было весьма расплывчатое. Что-то такое, что реализовано с помощью никому тогда не ведомого процессора, но только очень маленького, размером с копеечную монету. Живьем микропроцессор мало кто видел, только общие сведения: способен выполнять некоторые операции с двоичными векторами, достаточно быстро по сравнению с типовыми логическими элементами. Один раз, еще в Высшей Школе КГБ, нам, рассказывая про микропроцессоры того времени, сказали, что их стоимость сравнима со стоимостью золота, сопоставимого по весу с микропроцессором.
Сначала, как только я пришел на работу в отдел Степанова, там загорелись идеей создать специализированный криптографический процессор, ориентированный на выполнение определенных криптографических преобразований. Что это должны быть за преобразования – тоже не было единого мнения. Преобразования для системы с открытым распределением ключей? Или для симметричного шифрования, без которого система с открытым распределением ключей теряет всю свою эффективность? В общем, начальный период создания криптографического процессора прошел в абстрактных криптографических спорах, которые были спущены на грешную землю одним простым вопросом, заданным спорщикам инженером, приглашенным из Зеленоградского завода Ангстрем, на котором предполагалось изготавливать эти процессоры:
– А какой толщины должен быть слой лакового покрытия вашего процессора?
Все криптографы сразу же выпали в полный осадок. Ответить на вопрос о толщине слоя лакового покрытия никто не смог, абстрактный криптографический процессор, рожденный в умах теоретиков, так там и остался.
Но идеи шифров, реализуемых с не с помощью какого-то надуманного криптографического микропроцессора, а с помощью начинавших появляться в то время самых обычных микропроцессоров для портативной бытовой электроники, оказались весьма живучими. Все очень просто: есть выпускаемые промышленностью микропроцессоры, выполняющие стандартные арифметические операции, их производительность невелика, но они очень дешевы. Задача криптографов - приспособить эти стандартные процессоры для выполнения криптографических преобразований. Не гора должна идти к Магомету, а Магомет к горе.
Однажды к нам в гости пожаловали ребята из НИИ Автоматики. Это был один из ведущих институтов Министерства радиоэлектронной промышленности, который занимался разработкой шифрующих устройств и в котором работало много выпускников 4 факультета. В теории 8 управление КГБ должно было выполнять только экспертные функции, разработку шифраторов должна была проводить промышленность, но в реальной жизни все тесно переплеталось, наш отдел постоянно выдавал какие-то идеи для новых схем, масса людей писала на этом диссертации, поэтому провести четкую грань между разработкой и экспертизой часто было невозможно.
Эти ребята тоже занимались разработкой шифров на новой элементной базе. Но они были практиками, для них первичным было «железо», реально существующие в то время микропроцессоры, под которые надо было придумать криптосхему, в которой все преобразования осуществляются не с традиционными битами, а сразу с байтами, 8-мерными двоичными векторами.
– Мы постарались придумать максимально простую для реализации криптосхему. Вы можете прикинуть оценки ее стойкости?
Ребята молодые, может быть старше меня года на 3 - 4. Один из них уже начальник сектора, пишет диссертацию. Эта тема – шифры на новой элементной базе – интересует многих. На 4 факультете кафедра математики подготовила два солидных отчета о проведенных исследованиях по аналогичной теме, несколько человек уже защитились. Новое, перспективное направление, что же оно из себя представляло?
Здесь я вынужден извиниться перед читателем этой книги, не имевшим ранее никаких дел с математикой. Сейчас придется немного залезть в теорию групп и теорию подстановок, со своими специфическими терминами: симметрическая группа, циклическая подстановка, свойство 2-транзитивности и т.п. Может быть неискушенный читатель пробежит эту часть «по-диагонали», не вдаваясь особо в подробности и не забивая себе в голову всех этих премудростей. Но в математике, как и в любой другой области науки, иногда удается получить красивый результат, и, чтобы оценить его красоту, надо немного вникнуть в детали, подробности, предшествующие его получению. Так что читатель, окунувшийся в начинающиеся ниже математические дебри (не такие уж и сложные, как может показаться на первый взгляд!), в конце концов будет вознагражден одной красивой «изюминкой».
Большинство традиционных электронных шифраторов реализовано с помощью «балалаек», работающих с битами. В этих «балалайках» в ячейки регистра сдвига могут быть записаны только два элемента – 0 или 1, такой регистр сдвига называется регистром сдвига над полем GF(2) - полем Галуа из двух элементов. Операции с битами тоже весьма простые: сложение и умножение по модулю 2, а также отрицание. Все методы анализа подобных «балалаек» ориентированы на двоичные операции, на операции в поле GF(2).
Если же мы вместо битов переходим к байтам, то появляется много нового. Традиционные операции с байтами можно осуществлять несколькими способами. Например, сложение и вычитание могут быть с переносом или без переноса, т.е. или это будут операции в кольце вычетов по модулю 256, или покоординатное сложение бит. Но самое интересное обобщение происходит с операцией отрицания. Отрицание (инверсия) бита – это фактически подстановка на множестве из 2 элементов. Когда всего 2 элемента, то мощность симметрической группы S2 составляет всего 2! = 2, всего две подстановки: тривиальная единичная (ничего не меняется) и инверсия, когда 0 переходит в 1, а 1 – в 0. Мощность же симметрической группы S256 составляет 256! – совершенно фантастическое число. Введение подстановки в регистр сдвига, работающий с байтами, а не с битами, переворачивает все привычные методы криптографического анализа. Совершенно другие операции, а следовательно, нужны и другие подходы к анализу и оценке стойкости таких схем, чем те, которые использовались в традиционных двоичных «балалайках».
С чего начала кафедра математики на 4 факультете? С самого простейшего преобразования, осуществляемого с n-мерными двоичными векторами, с преобразования типа (GП)k, где G – группа, порожденная циклическим сдвигом (G = lt;ggt;, g =(0,1,…,2n-1)-циклическая подстановка), П - некоторая фиксированная подстановка из S2n, а k – некоторое целое число.
Если здесь перейти от математических терминов из теории групп к обычной криптографической терминологии, то преобразование типа (GП)k – это следующий узел.
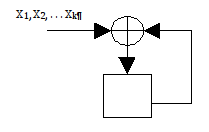 |
Преобразования типа (GП)k - это, фактически множество подстановок вида gx1П gx2П… gxkП, и задачей кафедры математики было обосновать какие-то свойства подобного множества, найти их зависимости от подстановки П. Типичная криптографическая ситуация – когда в таком узле
Кафедра начала с изучения группы lt;g, П gt;, т.е. группы, порожденной двумя подстановками: циклическим сдвигом g и фиксированной произвольной подстановкой П. Это естественное обобщение преобразования (GП)k, предельный случай. Свойства группы lt;g, П gt; дают ответ на вопрос, что в принципе можно ожидать от нашего преобразования при увеличении длины k до бесконечности. Можем ли мы таким путем получить все подстановки или же есть какие-то запреты?
Оказалось, что если случайно и равновероятно выбрать из всей симметрической группы фиксированную подстановку П, то с вероятностью, близкой к 1, группа lt;g, П gt; будет совпадать со всей симметрической группой, т.е. запретов не будет. Те подстановки П, для которых это не так, очень часто легко определяются, например, П=g, а также любая линейная подстановка, реализующая преобразование вида П(x) = ax+b, где a и b – фиксированные элементы из Z/2n.
Дальше, естественно, стали возникать вопросы: а как скоро мы сможем достичь симметрической группы? Какова будет мощность
За свойство 2-транзитивности взялись основательно, чувствовалось, что здесь могут быть интересные криптографические зацепки: если 2-транзитивность отсутствует, то появляются запреты переходов биграмм текста, широкое поле деятельности для криптоаналитика. Например, если П - упомянутая выше линейная подстановка, то для любой пары (y1,y2) будет справедливо соотношение:
П(y1)- П(y2) = (ay1+b) - (ay2+b) = a(y1-y2)
В этом случае при применении подстановки П сохраняется соотношение между разностями знаков, а поэтому кратной транзитивности заведомо не будет.
А если П - не линейная, а произвольная подстановка? При каком минимальном значении k множество (GП)k может достичь свойства 2-транзитивности? Всего имеется 2n(2n-1) различных пар (z1,z2), в которых z1lt;gt;z2, а количество различных подстановок в (GП)k не превосходит (2n)k. Следовательно, свойства 2-транзитивности можно достичь только при kgt;=2. Можно ли при k=2?
Рассмотрим множество подстановок (GП)2. Это множество реализует всевозможные преобразования произвольного значения t в значение s по формуле s = П (П (t+x1)+x2) при всевозможных x1,x2. Если бы это множество было 2-транзитивным, то для любых заранее фиксированных s1,s2, t1,t2 , в которых s1lt;gt;s2 и t1lt;gt;t2, система уравнений:
s1 = П (П (t1+x1)+x2)
s2 = П (П (t2+x1)+x2)
имела бы решение относительно x1,x2, а, следовательно, поскольку П - подстановка, то и система
s1 = П (t1+x1)+x2 (1)
s2 = П (t2+x1)+x2
имела бы решение для любых заранее фиксированных s1,s2, t1,t2, в которых s1lt;gt;s2 и t1lt;gt;t2
Отсюда, вычитая одно уравнение из другого, мы приходим к одной очень важной криптографической характеристики подстановки П - матрице частот встречаемости разностей переходов ненулевых биграмм P(П) размера (2n-1)x(2n-1), а именно, на пересечении i-ой строки и j-го столбца в этой матрице стоит значение pij - число решений системы уравнений относительно x и y:
x-y = i (2)
П(x) - П(y) = j
где i, j lt;gt; 0.
Если при каких-то i, j lt;gt; 0 pij =0, то это означает, что при заранее фиксированных s1,s2, t1,t2, в которых s1lt;gt;s2 и t1lt;gt;t2, а также t1-t2 = i, s1-s2 = j, система (1) заведомо не имеет решения, ибо в противном случае имела бы решение и система (2).
Заметим, что pij = p(2n-i)(2n-j). Действительно, каждому решению (x1,y1) системы (2) можно поставить во взаимно однозначное соответствие решение (x2,y2)=(y1,x1) системы
x-y = 2n-i
П(x) - П(y) = 2n-j
если домножить на –1 оба уравнения (2).
Из системы (2) очевидно вытекает, что число ее решений равно числу значений y, при которых
П(y+i) - П(y) = j (3)
Если каждому решению (x1,y1) системы (2) поставить во взаимно-однозначное соответствие пару (x2,y2) = (П-1(x1),П-1(y1)), то такая пара будет решением системы
x-y = j (4)
П-1(x) - П-1(y) = i
Следовательно, число решений системы (2) будет равно числу значений y, при которых
П-1(y+j) - П-1(y) = i (5)
Из (3) очевидно вытекает, что сумма всех элементов pij в i-ой строке при любом i равна 2n. Аналогично, из (5) вытекает, что сумма всех элементов pij в j-ом столбце при любом j равна 2n.
Поскольку размер P(П) равен (2n-1)x(2n-1), то из условия, что сумма всех элементов pij в i-ой строке при любом i равна 2n следует, что если бы P(П) не содержала нулей, то в любой ее строке все элементы были бы равны 1, кроме одного, равного 2. Аналогично получаем, что в этом случае в любом столбце должны быть все элементы 1, кроме одного, равного 2.
Если при некотором y выполняется
П(y+2n-1) - П(y) = 2n-1, (6)
то, поскольку 2n–2n-1 = 2n-1, то (6) будет справедливо и при значении y1 = y+2n-1. Таким образом, элемент p(2n-1)(2n-1) не может быть нечетным.
Предположим, что некоторая i-я строка целиком ненулевая. Это означает, что среди значений j0,j1,…,j2n-1, получаемых по формуле
jk =П(k+i)- П(k) (7)
содержатся все ненулевые элементы из Z/2n, а какой-то один элемент встретился ровно 2 раза.
Просуммируем соотношение (7) по всем k от 0 до 2n-1. Поскольку П - подстановка, то в правой части суммы получается 0, следовательно, сумма всех значений jk также должна быть нулевой.
Но среди j0,j1,…,j2n-1 содержатся все ненулевые элементы из Z/2n, а какой-то один элемент встретился ровно 2 раза. Поскольку сумма (по модулю 2n) всех ненулевых элементов кольца Z/2n равна 2n-1(2n-1) = 2n-1, то элементом, встретившимся два раза, должно быть 2n-1.
Тогда, в силу свойства pij = p(2n-i)(2n-j) для любого значения i должно выполняться
pi2n-1 = p(2n-i)2n-1 = 2
и при ilt;gt;2n-1 получается, что в 2n-1 столбце как минимум 2 элемента равны 2. Следовательно, если некоторая i-я строка при ilt;gt;2n-1 целиком ненулевая, то 2n-1 столбец заведомо содержит хотя бы один нулевой элемент, т.е. множество (GП)2 не является 2-транзитивным ни при какой подстановке П.
И еще отсюда сразу же вытекает, что общее число нулей в матрице P(П) не может быть меньше, чем 2n-3. В этом случае в матрице ровно две ненулевых строки, расположенных симметрично друг от друга, а в средней строке с номером 2n-1 ровно одно нулевое значение посередине: p(2n-1)(2n-1) = 0.
Подобными же методами легко показать, что в общем случае множество (GП)k является 2-транзитивным при kgt;2 в том и только том случае, когда матрица P(П)k-1 не содержит нулей. В частности, множество (GП)3 является 2-транзитивным тогда и только тогда, когда матрица P(П)2 не содержит нулей.
Стало ясно, в каком направлении вести математические раскопки теории шифров на новой элементной базе: изучать матрицы P(П) для различных подстановок П. Здесь сразу же выделялись плохие подстановки – это линейные преобразования вида
П(x) = ax+b
В этом случае при любом фиксированном ilt;gt;0 система (2) имеет решение только при одном значении jlt;gt;0, такая матрица заведомо не будет положительной ни в какой степени и свойство 2-транзитивности недостижимо. Число нулей у такой матрицы будет
А можно ли построить подстановки с
Но это больше теоретические дебри. С точки зрения практического применения гораздо важнее знать, чего можно ожидать от матрицы P(П) при случайном и равновероятном выборе П. И здесь были доказаны очень важные теоремы о том, что в среднем ненулевых элементов в этой матрице будет примерно 2/3, что с вероятностью, близкой к 1, при случайном и равновероятном выборе П матрица P(П)2 не будет содержать нулевых элементов, а группа lt;g,Пgt; будет совпадать с симметрической. В общем, все то, что требуется для использования подстановки П в качестве случайного разового ключа.
Вот такая была предыстория работ по шифрам на новой элементной базе. А ребята из НИИ Автоматики, по мотивам всех этих результатов, придумали следующую схему блочного шифра, работающего на основе байтового регистра сдвига и использующего только самые типовые операции с байтами, которые заложены в архитектуру появлявшихся тогда микропроцессоров. Эту схему назвали «Ангстрем-3».
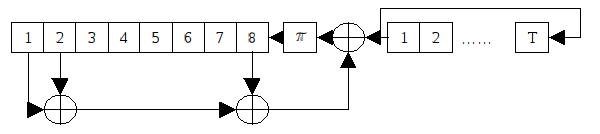 |
В ней два регистра сдвига, работающих с байтами. В первый регистр сдвига длиной 8 байт записывается 8-байтовый блок открытого текста, во второй – ключ, или как его еще можно здесь назвать входное слово, длины Т для первого регистра. Схема крутится Т тактов, после чего заполнение первого регистра выдается в качестве 8 байтового блока шифртекста. Типичный блочный шифр, все операции сложения – в кольце Z/256, реализация – изумительно простая, если писать программу, то это буквально две-три строки.
Но программы будут позже, а пока, в 1980 году, эту схему предполагалось реализовывать аппаратно, с помощью типовых микропроцессоров, работающих с байтами. Идеи подстановки-ключа тоже появятся позже, первоначально предполагалосьП выбрать и зафиксировать. А главный вопрос, который интересовал НИИ Автоматики – до какого предела можно уменьшать значение Т, количество тактов, которые должна отработать схема для зашифрования одного блока. Чем меньше Т, тем выше скорость шифрования, а это было для них определяющим фактором.
– Нельзя ли выбрать Т=16?
Нужно подумать.
Так начиналась моя осмысленная работа в Теоретическом отделе. Перед глазами - чистая тетрадь, отчеты 4 факультета и НИИ Автоматики, сиди и думай, нельзя ли выбрать Т=16.
| © 2025 Библиотека RealLib.org (support [a t] reallib.org) |