"Кристаллы" - читать интересную книгу автора (Китайгородский Александр Исаакович)
3. Что такое симметрия
Смысл этого слова лучше всего мы поймём на примерах.
На рисунке 5,
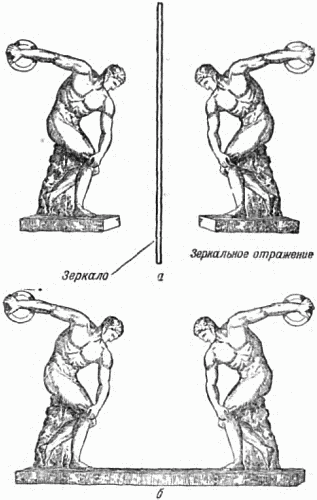 |
Рис. 5.
Действительно, представим себе, что так же, как и на рисунке 5,
На рисунках 6 и 7 приведены другие примеры тел, имеющих плоскость симметрии. Плоскостью симметрии обладают тела животных, вертикальную плоскость симметрии можно провести через человека. В животном мире симметрия осуществляется лишь приблизительно, да и вообще идеальной симметрии в жизни не существует. Архитектор может изобразить на чертеже дом, состоящий из двух идеально симметричных половин. Но когда дом будет построен, как бы хорошо его ни делали, всегда можно будет найти разницу в двух соответствующих частях здания: в одном месте есть трещинка, в другом – нет; в одном месте краска положена густо, в другом редко…
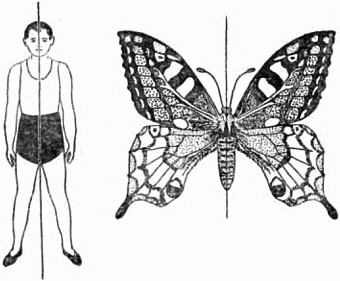 |
Рис. 6. Зеркальную плоскость симметрии имеют тела человека и животных.
 |
Рис. 7. Здание Московского Государственного Университета им. М.В. Ломоносова обладает вертикальной плоскостью симметрии.
Наиболее точная симметрия осуществляется в мире кристаллов, но и здесь она не идеальная: наличие невидимых глазом трещинок, царапин всегда делает равные грани слегка отличными друг от друга.
На рисунке 8 изображена детская бумажная вертушка. Она тоже симметрична, но плоскость симметрии через неё провести нельзя. В чём же тогда заключается симметрия этой фигурки? Прежде всего, спросим себя о симметричных её частях. Сколько их? Очевидно, четыре. В чём заключается правильность взаимного расположения этих одинаковых частей? Это также нетрудно заметить. Повернём вертушку на прямой угол, то есть на 1/4 окружности; тогда крыло
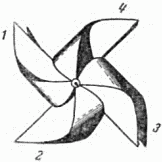 |
Рис. 8. Бумажная вертушка обладает осью симметрии 4-го порядка.
Итак, ось симметрии – это такая прямая линия, поворотом около которой на долю оборота можно перевести тело в положение, неотличимое от исходного. Порядок оси (в нашем случае 4-й) указывает, что такое совмещение происходит при повороте на 1/4 окружности. Следовательно, четырьмя последовательными поворотами мы возвращаемся в исходное положение.
Оси симметрии различных порядков приблизительно осуществляются у цветов. Цветок на рисунке 9,
 |
Рис. 9. Оси симметрии 2-го и 6-го порядков у цветов.
На рисунке 10 приведены примеры более сложных случаев симметрии, встречающихся в природе. Организм на рисунке 10,
 |
Рис. 10. Примеры более сложной симметрии, осуществляемой природой.
Снежинка на рисунке 10,
Встречаемся ли мы с симметрией любого типа в царстве кристаллов? Опыт показывает, что нет.
В кристаллах мы встречаемся лишь с осями симметрии 2, 3, 4 и 6-го порядков. И это не случайно. Кристаллографы доказали, что это следует из решетчатого строения (см. ниже) кристалла. Поэтому число различных видов или, как говорят,
| © 2024 Библиотека RealLib.org (support [a t] reallib.org) |